Тепловое подо6ие

Поскольку аналитическое определение значения коэффициента теплоотдачи α является достаточно сложной проблемой, для этой цели прибегают к экспериментальным исследованиям с использованием теории подобия. Полученные в этом случае результаты могут быть с высокой степенью достоверности распространены на широкий диапазон подобных процессов.

Анализ дифференциальных уравнений, описывающих процесс конвективного переноса теплоты с позиций теории подобия, по­зволил получить критерии, приведенные в табл. 5.1

Следует обратить внимание, что критерий Пекле является произведением критериев Рейнольдса и Прандтля 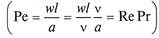, поэтому при описании тепловых процессов вместо него чаще используют произведение критериев гидромеханического Rе и теплового Pr подобия.

Полученные критерии подобия позволяют записать общее критериальное уравнение конвективного переноса теплоты

f(Re, Gr, Nu, Pr, Fo) = 0.

Определяемым критерием, который нельзя определить из условий однозначности, является критерий Nu, содержащий искомый коэффициент теплоотдачи. Остальные критерии являются определяющими:

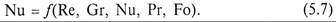
Уравнение (5.7) в зависимости от условий проведения процесса теплообмена может быть упрощено. Так, если процесс является стационарным, из него выпадает критерий Fo. Поскольку критерии Rе и Gr характеризуют различные гидродинамические режимы (вынужденной и естественной конвекции), чаще всего для конкретных условий используется только один из них.

Таким образом, для стационарных процессов теплообмена при вынужденной' конвекции уравнение (5.7) запишется

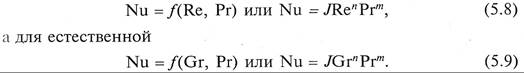
В выражениях (5.8) и (5.9) j, n, m – экспериментальные коэффициенты, определяемые для конкретных систем и условий теплоотдачи.

В качестве примера рассмотрим ряд экспериментальных критериальных уравнений, описывающих различные случаи конвективной теплоотдачи.

Теплоотдача при свободном движении жидкости характеризуется уравнением (5.9), которое в этом случае принимает вид

где с и n – константы, численные значения которых выбирают в зависимости от произведения GrPr (табл. 5.2).

Физические параметры, входящие в формулу (5.10), определяются при средней температуре t_cp = 0,5(t_ср + t_f).

Теплоотдача при вынужденном движении жидкости зависит от характера этого движения (развитое турбулентное течение, неустойчивое турбулентное течение, ламинарное течение).

Развитое турбулентное течение (Re > 10^-4). Теплоотдача в этом случае зависит от характера движения и физических свойств жидкости

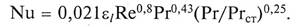
Здесь определяющая температура – средняя температура жидкости, а для критерия Рг, все физические величины берутся при температуре стенки.

Коэффициент теплоотдачи в коротких трубах и каналах несколько больше, что учитывается поправочным коэффициентом ε_l (табл. 5.3).

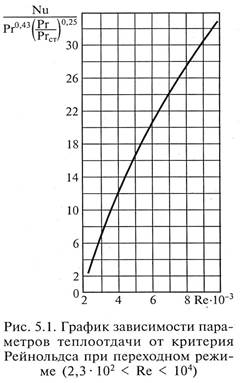
Неустойчивое турбулентное течение в переходной области (2,3*10² < Re < 10⁴) можно описать либо приближенной формулой

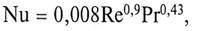
либо графической зависимостью (рис. 5.1).

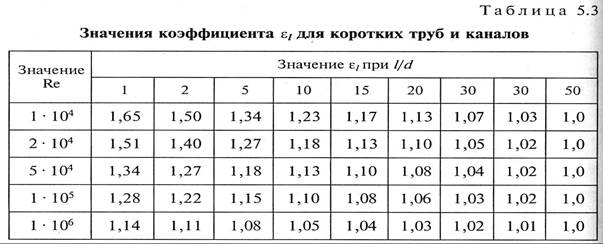
Ламинарный режим течения характеризуется тем, что вследствие разности температуру стенки и в ядре потока на основное движение жидкости накладывается естественная конвекция. Интенсивность теплоотдачи при этом усиливается, а в уравнение дополнительно входит критерий Грасгофа:

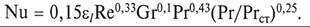
Теплоотдача в аппаратах с мешалкой. Для повышения интенсивности теплообмена в аппаратах со змеевиками и рубашками используют мешалки. В этом случае значения коэффициентов теплоотдачи зависят от конструкции аппарата и мешалки, а также физических свойств перемешиваемой среды. Для расчета можно воспользоваться упрощенными уравнениями:

·

Nu = 0,36*Re_м^0,67*Pr^0,33;

· при теплообмене со змеевиком

Nu = 0,87* Re_м^0,67*Pr^0,33.

Теплоотдачу при изменении агрегатного состояния жидкости можно разделить на теплопередачу при кипении жидкости и теплоотдачу при конденсации пара (подвижного и неподвижного).

Теплоотдача при кипении жидкости. Кипение - процесс интенсивного парообразования, происходящего во всем объеме жидкости, перегретой относительно температуры насыщения с образованием паровых пузырей.

Режим кипения, при котором пар образуется в виде отдельных периодически зарождающихся, растущих и отрывающихся паровых пузырей, называется пузырьковым кипением.

Режим кипения, при котором происходит слияние о6разуюпщхся пузырьков в подвижную паровую пленку, поднимающуюся у поверхности нагрева, называется пленочным кипением.

Коэффициенты теплоотдачи при пузырьковом кипении выше, чем при пленочном кипении.

Коэффициент теплоотдачи для кипящей жидкости может быть рассчитан по уравнению, связывающему коэффициент теплоотдачи с тепловым потоком и физическими свойствами жидкости:

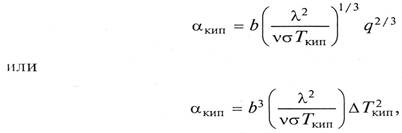
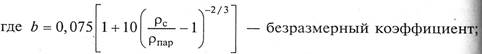
ρ_с, ρ_пар – плотности среды и пара, кг/м³; ν – кинематическая вязкость, м²/с; λ – коэффициент теплопроводности, Вт/(м*К); σ – поверхностное натяжение, Н/м; Т_кип – температура кипения, К; ΔТ_кип = Т_ст – Т_кип – движущая сила процесса теплоотдачи, К; q – удельная тепловая нагрузка, Вт/м2.

Все физико-химические константы следует брать при температуре кипения.

Теплоотдача при конденсации пара. Если пар соприкасается со стенкой, температура которой ниже температуры насыщения, то он конденсируется на ней. Различают три вида конденсации пара на твердой поверхности:

· пленочная конденсация, когда конденсат стекает по поверхности в виде сплошной пленки;

· капельная конденсация, когда конденсат выпадает на поверх­ности в виде отдельных капель;

· смешанная конденсация, когда часть поверхности покрыта каплями, а часть – пленкой конденсата.

В результате гидродинамического и теплового анализа процесса пленочной конденсации пара получена формула

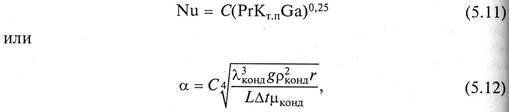
где 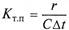- критерий теплового подобия при изменении агрегатного состояния; С – коэффициент, равный 0,94 для конденсации пара на вертикальной стенке или трубе и 0,74 —для конденсации на горизонтальной трубе; λ_конд, ρ_конд,μ_конд – параметры конденсата при средней температуре пленки t_cp = 0,5(t_s + t_ст); t_s – температура насыщения пара; L – определяющий размер (для вертикальной стенки — высота, для горизонтальной трубы – диаметр).

Формулы (5.11) и (5.12) получены для случая конденсации неподвижного пара. Для движущегося пара значение коэффициента теплоотдачи может быть либо больше, либо меньше по сравнению с неподвижным.

Зависимости для расчета коэффициентов теплоотдачи для различных условий и конструкций аппаратов можно найти в справочной литературе.

Тепловое излучение характеризуется длинами волн, которые лежат в невидимой (инфракрасной) части спектра и имеют длину 1),8...40 мкм.

При попадании на тела лучистая энергия частично поглощается Qпогл, частично отражается Qотр, частично проходит сквозь них Qпр:

Q_л = Q_погл+ Qотр+ Qпр

Поглощаемая телом часть лучистой энергии переходит в тепловую, а отраженная и прошедшая сквозь него может поглощать­ся другими телами.

Если рассматривать долю каждой энергии в общем количестве лучистой энергии

1 = Q_погл/Q_л + Q_отр/Q_л + Q_пр/Q_л

то в случае, если:

· Q_погл/Q_л = 1 (вся энергия поглощается), тело называется абсолютно черным;

· Q_отр/Q_л = 1 (вся энергия отражается), тело называется абсолютно белым;

· Q_пр/Q_л = 1 (вся энергия проходит сквозь тело), тело называется абсолютно прозрачным (или диатермичным).

Тела, имеющие все три доли, называют серыми телами. Основные закономерности процесса теплового излучения могут быть описаны с помощью следующих законов.

Закон Стефана – Больцмана. Лучеиспускательная способность серого тела Е пропорциональна четвертой степени его температуры Т, К, и коэффициенту лучеиспускания серого тела С:

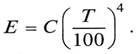
Сопоставив энергию излучения серого тела с энергией излучения абсолютно черного тела при той же температуре, получим относительную излучательную способность (степень черноты) тела

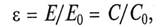
где Е₀ – лучеиспускательная способность абсолютно черного тела;

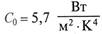- коэффициент лучеиспускания абсолютно черного тела.

Закон Кирхгофа. Согласно этому закону поглощательная способность и степень черноты равны между собой:

ε = А,

где А – отношение поглощаемой телом лучистой энергии к общему ее количеству, падающему на тело.

Из закона Кирхгофа следует, что лучеиспускательная способность тела тем выше, чем больше его поглощательная способность. Этими объясняется наивысшая лучеиспускательная способность абсолютно черного тела, так как для него А = 1, а следовательно, и ε = 1.

Наоборот, тела, хорошо отражающие лучистую энергию, сам излучают мало, а для абсолютно белого и абсолютно прозрачного тел лучеиспускательная способность равна нулю.

Теплообмен лучеиспусканием между телами. Количество теплоты, отданной телом с абсолютной температурой Т₁ окружающим более холодным телам с абсолютной температурой Т₂, составляет

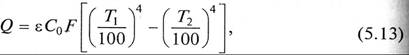
где F - условная расчетная поверхность теплообмена.

Совместная передана теплоты конвекцией и лучеиспусканием. Передача теплоты лучеиспусканием обычно сопровождается одновременной передачей теплоты конвекцией. Пусть от стенки с абсолютной температурой Т_ст теплота передается к среде с абсолютной температурой Тf(соответствующие температуры в °С будут t_ст и t_f)

Теплота, передаваемая конвекцией, в соответствии с формулой (5.6) при стационарном режиме составит

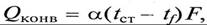
а теплота, передаваемая лучеиспусканием, в соответствии с (5.13) составит

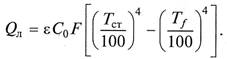
Общее количество передаваемой теплоты равно

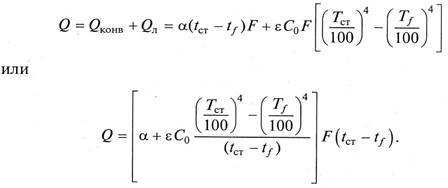
Второй член выражения, заключенного в квадратные скобки, называется коэффициентом теплоотдачи при лучеиспускании α_л. Таким образом

где (α+α_л) – общий коэффициент теплоотдачи (при совместной передаче теплоты конвекцией и лучеиспусканием).