Гармоническое колебание.

Прикрепим к равномерно вращающемуся диску шарик на стержне и осветим его сбоку на экран. При вращении диска тень шарика будет колебаться взад и вперед. На рис.1.3 отмечены и занумерованы 16 последовательных положений шарика, взятых через каждую 1/16 полного оборота. Теми же цифрами от 1 до 16 занумерованы положения тени на экране АВ; эти точки получены путем опускания на прямую АВ перпендикуляров из точек окружности. Именно так проектируется тень на экран, если шарик освещать пучком параллельных лучей.

Для того чтобы развернуть колебания проекции шарика подобно тому, как это делает зеркальный барабан, построим ряд равноотстоящих друг от друга прямых, параллельных АВ. Последовательные положения проекции (тени) 1, 2, 3, …16 мы наносим не на одной и той же прямой, а на следующих друг за другом. Проведя через отмеченные таким способом точки непрерывную кривую, находим волнистую линию, указывающую последовательные положения шарика, т.е. график его движения. Таким образом, мы получим «осциллограмму» колебаний проекции шарика.

Колебание, какое совершает при равномерном движении точки по окружности проекция этой точки на какую-либо прямую, называется гармоническим (или простым) колебанием. Гармоническое колебание является, таким образом, специальным, частным видом периодического колебания. Этот специальный вид колебания очень важен, так как он чрезвычайно часто встречается в самых различных колебательных системах.

Заметим, что в определении гармонического колебания речь идет о параллельной проекции, т.е. положения точки, движущейся по окружности, сносятся на прямую АВ (рис.1.3) посредством параллельных между собой перпендикуляров к АВ.

Если на горизонтальной оси откладывать центральный угол α (рис. 1.4), а на вертикальной ВВ¹, опущенный из конца вращающегося радиуса ОВ на неподвижный диаметр АА¹ (угол α отсчитывается от неподвижного радиуса ОА), то получится кривая, называемая синусоидой. Для каждой абсциссы α ордината этой кривой ВВ¹ пропорциональна синусу угла α, так как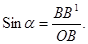

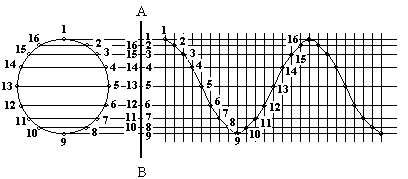Рис.1.3. Построение развертки гармонического колебания.

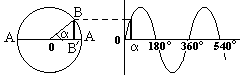Рис.1.4. Построение синусоиды.

Сравнивая это построение с только что описанным построением развертки гармонического колебания, нетрудно усмотреть их полное тождество. Таким образом, «волнистая кривая», изображающая гармоническое колебание, есть синусоида. Поэтому очень часто гармоническое, или простое, колебание называют также синусоидальным колебанием.

Число циклов гармонического колебания, совершенных за 1 сек, называется частотой этого колебания. Если период маятника равен 1 сек (секундный маятник), то за 1 сек совершается один цикл и частота равна единице. Единицу частоты называют циклом в сек, или герцем (сокращенно гц). Как обычно, приставки кило и мега обозначают в тысячу и в миллион раз более крупные единицы:

1 килогерц (1 килоцикл в сек) = 1000 герц,

1 мегагерц (1 мегагерц в сек) = 1000000 герц = 1000 килогерц.

Если период равен 5 сек, то частота будет 1/5 герца. Обозначая продолжительность периода, выраженного в секундах, через Т, а частоту, выраженную в герцах через f, будем иметь:

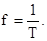
Однако следует помнить, что такая связь между частотой и периодом характеризует только гармоническое (синусоидальное) колебание. Поэтому, когда мы говорим о колебании с определенной частотой, то при этом всегда понимается гармоническое колебание, а не периодическое движение произвольной формы.