ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ПОЛЕЗНОСТИ
Пусть L - лотерея, которая приводит к выигрышам (действиям) х1, х2,…, хn с соответствующими вероятностями p1, p2, …, pn, и соответствующими полезностями U(X1), U(X2), … U(Xn).
Обозначим ожидаемый выигрыш (математическое ожидание выигрыша) через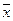 
:
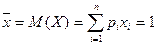(1)
Математическое ожидание полезности, т.е. ожидаемую полезность выигрыша, определяют по формуле:
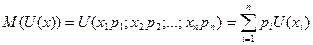, (2)
т.е. полезность набора результатов совпадает с математическим ожиданием полезности результатов.
Определение: ожидаемая полезность события равна сумме произведений вероятности исходов на значение полезностей этих исходов.
Детерминированный эквивалент лотереи. Страховая сумма
Взаимосвязь риска с полезностью определяется понятием детерминированного эквивалента лотереи.
Детерминированный эквивалент лотереи L— это гарантированная сумма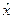 
, получение которой эквивалентно участию в лотерее и гарантирует ЛПР такую же самую полезность, как и участие в рискованном деле, то есть 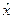~ L. т.е. 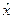определяется из равенства:
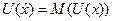или 
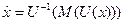, (3)
где U-1— функция, обратная к функции U(х).
Премию (надбавку) за риск в лотереи определяют как разницу между ожидаемым выигрышем и детерминированным эквивалентом.
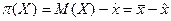. (4)
По своему физическому смыслу премия за риск (надбавка за риск) p (Х)— это сумма (в единицах измерения критерия х), которой ЛПР согласен пожертвовать (уступить ее) из среднего выигрыша (т.е. эта сумма меньше, чем математическое ожидание выигрыша), чтобы избежать риска, связанного с лотереей, и получить гарантированный доход.
Перед ЛПР может стать проблема, которая состоит в том, что ЛПР стремится отказаться от лотереи, которая менее привлекательная, чем состояние, в котором пребывает ЛПР. В этом случае возникает вопрос, сколько б ЛПР заплатил (в единицах измерения), чтобы не участвовать в лотереи (избежать ее). Эту величину называют страховой суммой.
Страховой суммой (СС) называют величину детерминированного эквивалента, взятую с противоположным знаком:
СС(Х) = - 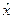. (5)
ВЫВОДЫ
Дата добавления: 2015-08-14; просмотров: 1686;