Дифференцирование сложных функций.
Теорема 9. Пусть 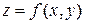 – функция, дифференцируемая в точке
– функция, дифференцируемая в точке 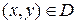 ,
, 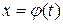 и
и 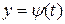 – дифференцируемые функции независимой переменной
– дифференцируемые функции независимой переменной 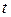 . Тогда производная сложной функции
. Тогда производная сложной функции 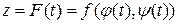 вычисляется по формуле
вычисляется по формуле
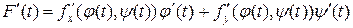
или (в другой форме записи)
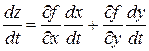 . (2)
. (2)
Формулу (2) можно распространить на случай, когда 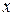 и
и 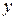 – функции двух переменных
– функции двух переменных 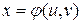 ,
,  :
:
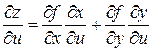 ,
, 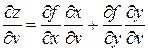 . (3)
. (3)
Пример. Найти  , если
, если 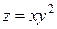 ,
, 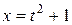 ,
, 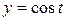 . По формуле (2) имеем
. По формуле (2) имеем
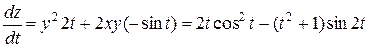 .
.
Пример. Найти 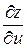 и
и 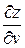 , если
, если 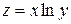 ,
, 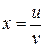 ,
, 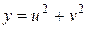 . По формулам (3) имеем
. По формулам (3) имеем
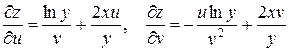 .
.
В эти выражения следует подставить 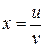 ,
, 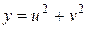 .
.
Дата добавления: 2015-08-14; просмотров: 766;
