Построение структурных карт

Имея динамические, либо кинематические глубинные сейсмические разрезы увязанных между собой в точках их пересечения и зная положение профилей на поверхности наблюдений, можно построить структурные карты или схемы в виде изолиний равных абсолютных отметок залегания различных отражающих горизонтов в пределах изученной площади.

Вначале строится структурная карта для наиболее мелкой отражающей границы раздела, затем до следующей более глубокой и т.д. Интерполяция между точками с известными координатами залегания отражающей поверхности вдоль профилей и по площади должна производиться так, чтобы не нарушалось условие ортогональности нормальных лучей и отражающей поверхности.

В настоящее время существует математическое обеспечение, позволяющее использовать параметры наблюденных отраженных волн для автоматического построения карт изохрон отражений, а также линий равных значений v_эфф, v_ср и v_пл для пересчета карт изохрон в структурные карты и оценить достоверность полученных карт. При построениях структурных карт обычно выделяют следующие этапы.

Увязка глубин по профилям: глубины залегания отражающих границ и их конфигурация определяются по данным сейсморазведки с погрешностями, зависящими от многих факторов. Основные источники погрешностей зависят от того, в какой степени принятая при интерпретации скоростная модель среды близка к реальной, с какими погрешностями были определены поправки за рельеф земной поверхности, неоднородное строение верхней части разреза до линии приведения.

Оценка точности структурных построений: выбор сечения и масштаба структурной карты

Точность структурных построений складывается из дисперсий погрешностей определения глубин и ошибки интерполяции:

.

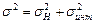Прогнозная оценка точности структурных построений по системе профилей (или одному профилю) характеризуется дисперсией погрешностей определения глубин исследуемого горизонта σ_Н² (ошибка метода) и зависит от:

- используемой при интерпретации модели среды;

- ошибок измерения кинематических параметров (времени и скорости);

- истинная модель среды при интерпретации, как правило, неизвестна и поэтому в полной мере не может быть учтена при прогнозной оценке точности структурных построений. В лучшем случае известен наиболее целесообразный в конкретных условиях вид аппроксимации среды.

Способ оценки точности структурных построений должен выбираться для той аппроксимирующей модели, в рамках которой происходит интерпретация материалов. Рассматриваются три основные аппроксимирующие модели среды:

а. модель среды, описываемая средними скоростями;

б. пластовая модель среды;

в. смешанная модель среды, когда до определенного горизонта среда характеризуется средними скоростями, а ниже - пластовыми.

Дисперсия σ_Н² погрешностей глубин 1-ого горизонта (r=2-1, 2,…) в рамках модели средних скоростей оценивается следующим образом:

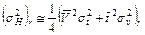(1),

где V среднее по площади или профилю значение средней (эффективной) скорости в толще, покрывающей r-ый горизонт; σ²_v - дисперсия погрешностей средних (эффективных) скоростей до r-ого горизонта; 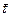- среднее по площади или профилю значение двойного времени σ_t² - дисперсия погрешностей времени t для r-го горизонта.

Параметр 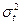включает три компоненты:

- погрешность измерения времени t (погрешнооть t_M), характеризуемая дисперсией 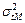отклонений времен t горизонта от плавной усредняющей их линии или поверхности;

- погрешность корреляции волн tк характеризуемая дисперсией ;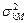

- погрешность статических поправок за глубину линии приведения t₀, описываемая дисперсией :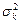

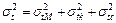(2),

Дисперсия 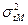является следствием влияния случайных волновых помех и остаточного фона регулярных волновых помех на временных разрезах МОВ ОГТ, случайного не откорректированного разброса времён и амплитуд суммируемых волн, погрешностей снятия времён отражающего горизонта с временных разрезов и т.д. При хорошем качестве материала, обеспечивающим возможность непрерывного прослеживания волн по замкнутым контурам, дисперсия 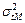оценивается как дисперсия неувязок времен t отражающего горизонта в точках пересечения профилей после увязки сети по одной фазе. Погрешности корреляции проявляются при случайном переходе с фазы на фазу под воздействием погрешностей t_M и могут быть, вызваны влиянием интерференции волн на временном разрезе, изменением свойств отражающих границ и т.д.

Дисперсия ошибок корреляции приближенно определяется как:

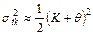(3),

где θ - период коррелируемой волны на временном разрезе, К - показатель качества корреляции устанавливаемый интерпретатором; К=0 при уверенном прослеживании фазы волны; К=1 при групповой корреляции в рамках двух фаз; К=2 при групповой корреляции в рамках трех фаз и т.д.

Величина погрешности статических поправок зависит от строения зоны малых скоростей (ЗМС) и расположения точки возбуждения сейсмических волн. В случае спокойного рельефа и простого строения ЗМС, когда точность расчета статических поправок высока (погрешность - 2-4 мсек), дисперсией 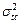в формуле можно пренебречь.

Дисперсия погрешностей средних (эффективных) скоростей определяется различными способами в зависимости от методики структурных построений. В случае использования для построений отдельных значений эффективных скоростей V(х) вычисляемых по профилям, дисперсия может быть найдена через разброс скоростей в точках пересечения профилей. Эту же величину характеризует дисперсия отклонений 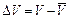эффективных скоростей от сглаженных их значений .

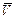Прогнозная оценка точности построений для r-ого горизонта в рамках пластовой модели среды (σ²_М) оценивается, как

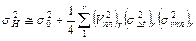(4),

где r=0,1,2, ... - номер пласта или горизонта, связанного с его подошвой, σ²_Н дисперсия погрешностей определения глубин r-ого горизонта; σ²₀ - дисперсия погрешностей построений глубин верхнего горизонта (r=0), ниже которого построения осуществляются с использованием пластовой модели среды; ( 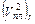- среднее значение скорости в r пласте 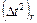средняя временная мощность r-ого пласта; 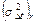- дисперсия погрешности определения временной мощности r-ого пласта; 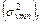- дисперсия погрешности определения пластовой скорости в r-ом пласте. Если верхний (нулевой) горизонт строится по обобщенным данным, то σ²₀ определяется по формуле (1). Если построения верхнего горизонта (подошва ВЧР) осуществляется на основе данных структурного бурения, то σ²₀ определяется как точность этого горизонта по данным бурения.

Дисперсия погрешностей определения параметра 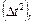, складывается из дисперсий погрешностей определения времени r-ого и (r - 1)-ого горизонтов:

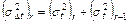(5).

Оценка точности пластовой скорости 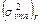для r-ого пласта зависит от способа определения скоростей. В случае наличия большого (более 6 - 5) количества скважин с данными сейсмокаротажных наблюдений в районе с резко выраженными структурными формами и значительными колебаниями глубин исследуемого горизонта по площади для сейсмических построений используются осредненные графики изменения пластовых скоростей в зависимости от глубины залегания пласта 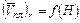. В качестве меры точности определения пластовых скоростей используются дисперсия разброса единичных определений 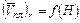полученных в разных точках района, вокруг осредненного графика 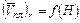. При определении пластовой скорости путём решения прямой и обратной кинематической задачи оценка дисперсии производится по различию скоростей в узлах пересечения профилей и отклонением осредняющей линии пластовой скорости от единичных определений.

Дисперсия погрешностей интерполяции характеризуется выражением:

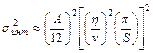(6),

где A - амплитуда структуры; S - площадь структуры; η - параметр, приближенно равный 2,5; v - плотность сети профилей (км/км²).