Арифметические операции.
Все четыре арифметические операции над двоичными числами сводятся фактически к двум операциям сложению и сдвигу. Это позволяет технически реализовать четыре действия арифметики в одном арифметически- логическом.
В современных компьютерах минимальной единицей информации является байт, который всегда контролируется контрольным разрядом.
Контрольный Номера битов
 бит
бит
 |
Номер 7 6 5 4 3 2 1 0








 разряда
разряда
128 64 32 16 8 4 2 1
7 6 5 4 3 2 1 0









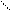
 (+) 64 32 16 8 4 2 1
(+) 64 32 16 8 4 2 1
 | |||
 | |||
Бит Вес двоичной позиции
Знак
7 6 5 4 3 2 1 0
 |

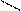

(-) Запись дополнительного кода
Рис 2.2.Изображение регистра МП или ячейки
Памяти
Пример *25 Умножение 25*8 заменим операцией
58 Сложения 25 + 25 + … + 25 =200
200 

 8 раз
8 раз
125  сдвигаем множитель вправо на 1 раз
сдвигаем множитель вправо на 1 раз
1450 25*5 заменим операцией сложения
25 + 5раз + 25 = 125
Отсюда выводлюбую арифметическую операцию можно представить в виде нескольких сдвинутых относительно друг друга слагаемых. При выполнении арифметических операций в компьютере применяется прямой, обратный и дополнительный коды:
Прямой код - при умножении и делении
Обратный код - при вычитании
Дополнительный код – при сложении положительных и отрицательных чисел.
Пример:
 Умножение Деление
Умножение Деление
1011 


 110010 1010
110010 1010
 1101 1010 101
1101 1010 101


 1011 001010
1011 001010



 0000 1010
0000 1010

 1011 0000
1011 0000
 1011
1011
 10001111
10001111
Прямой коддвоичного числа – само двоичное число, причем значения знакового разряда для положительных чисел равно 0, а для отрицательных 1.
 + 0,1101 0,1101
+ 0,1101 0,1101
-  0,1101 1,1101
0,1101 1,1101
Обратный код положительного числа совпадает с прямым кодом, а для отрицательных чисел, все цифры числа заменяются на противоположные значения.
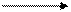 + 0,1101 0,1101
+ 0,1101 0,1101
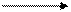 - 0,1101 1,0010
- 0,1101 1,0010
Дополнительный код положительного числа совпадает с прямым кодом. Дополнительный код отрицательного числа образуется как результат суммирования обратного кода с единицей младшего разряда.
+ 0,1101 доп. Код 0,1101
- 0,1101 доп. Код 1,0010
+ 1
 |
1,0011
Компьютер обрабатывает информацию в двоичном коде.
Но если надо использовать числа со знаком, используется дополнительный код, что упрощает аппаратуру компьютера.
| Десятичные | Представление чисел | Примечание |
| + 127 | 0 1 1 1 1 1 1 1 | Положительные числа - |
| . . . | . . . | представлены в |
| + | 0 0 0 0 0 0 1 1 | той же форме что |
| +2 | 0 0 0 0 0 0 1 0 | и прямые |
| +1 | 0 0 0 0 0 0 0 1 | двоичные числа |
| +0 | 0 0 0 0 0 0 0 0 | |
| -1 | 1 1 1 1 1 1 1 1 | Отрицательные |
| -2 | 1 1 1 1 1 1 1 0 | числа - |
| -3 | 1 1 1 1 1 1 0 1 | представлены в |
| . . . | . . . | форме |
| дополнительного | ||
| - 128 | 1 0 0 0 0 0 0 0 | кода |
Рис 2.2 Представление чисел со знаком
Вопросы к лекции
5. Как устроена разрядная сетка двоичной системы счисления, и из каких элементов она состоит?
6. Как выглядит разрядная сетка 8-ми разрядного микропроцессора или ячейка памяти длиной в один байт?
7. Как изображается число со знаком в 8-ми разрядной ячейке памяти?
8. Что такое двоично-десятичный код ( ДДК) и как в нем закодированы десятичные цифры?
9. Каким способом в компьютере выполняются четыре действия арифметики?
10. Как образуется прямой код двоичного числа, и какие значения может принимать знаковый разряд числа?
11. Как образуется обратный код положительного двоичного числа и обратный код отрицательного двоичного числа?
12. Как образуется дополнительный код положительного и отрицательного двоичного числа?
Дата добавления: 2015-08-14; просмотров: 868;
