Лекция № 27

Вычисление суммы бесконечного убывающего ряда с заданной точностью. Итерационные циклы. Задача сводится к нахождению суммы

,

каждое слагаемое, которой является функцией от номера n, определяющего место этого слагаемого в сумме, а также может являться функцией одного или нескольких дополнительных параметров.

Вычисление суммы ряда состоит в получении в результате циклического процесса последовательности u(1), u(2), ..., u(n), ..., сходящейся к своему предельному значению, т. е. 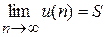. Здесь u(n) – сумма n членов бесконечного ряда.

Для вычисления суммы ряда используется рассмотренный выше прием накопления суммы: суммирование считается законченным при выполнении условия достижения заданной погрешности e: 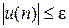. Задача нахождения суммы ряда является типичным примером итерационного процесса, так как заранее не известно, при каком числе членов ряда будет достигнута требуемая точность.

Процесс вычисления определяется рекуррентным соотношением (т.е. к предыдущему значению прибавляется текущее) u(n)=u(n-1)+u(n). Алгоритм нахождения суммы ряда показан на рис 9.8.

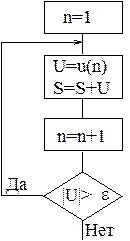
Рис. 9.8. Вычисление суммы ряда

В приведенной блок-схеме для вычисления суммы ряда используется рассмотренный выше прием накопления суммы. Только теперь суммирование считается законченным тогда, когда выполнится условие – значение члена ряда станет меньше заданной погрешности e: .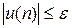

Для организации такого итерационного цикла (т.е. цикл с заранее неизвестным числом повторений) применяется оператор Do...Loop. Именно здесь проявляется удобство этого оператора, поскольку, используя, оператор For...Next, поставленную задачу решить не удается – For...Next – оператор цикла с заранее заданным числом повторений.

Пример 20. Составить программу вычисления приближенного значения числа p, используя равенство

.

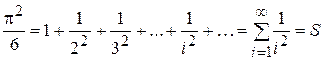Вычисления закончить, когда значение последнего члена ряда не станет меньше 0, 0000001. Определить длину приближенного ряда.

Из условия задачи задаем погрешность e = 0, 0000001. Число p находим по формуле 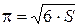, где S – сумма ряда, которую необходимо вычислить. Для поиска суммы S применим цикл “ДО” с постусловием.

Sub Demo_Pi()

Dim i As Integer

Dim e, s, u, Pi As Single

i = 1

s = 0

' Задаем точность вычисления

e = 0.0000001

Do

' Вычисляем значение текущего члена ряда

u = 1 / i ^ 2

s = s + u

i = i + 1

Loop Until Abs(u) < e

Pi = Sqr(s * 6)

MsgBox "Число Пи равно " & Pi & ", число итераций равно " & i - 1, , "Решение задачи"