Назначение метода интегрирования
Назначение метода интегрирования означает, что для расчетов ко всем интеграторам блок-схемы ("1/S") подключается указанный алгоритм. Если Вы выбираете адаптивный алгоритм, то дополнительно необходимо определить минимальный размер шага, допуск ошибки и количество возможных итераций.
VisSim имеет семь алгоритмов интегрирования различной точности для численного решения (интегрирования) дифференциальных уравнений: Эйлера, Трапециидальный, Рунге-Кутта 2-ого порядка, Рунге-Кутта 4-ого порядка, Адаптивный Рунге-Кутта 5-ого порядка, Адаптивный Булирша-Стоера и Обратный Эйлера (жесткий).
Каждый алгоритм является численным приближением к идеализированному, непрерывному интегрированию. По сути, приближение базируется на балансе между скоростью выполнения и точностью. В целом, более сложные алгоритмы более устойчивы и численно более точны; однако, требуют больших вычислительных ресурсов.
Для визуальной демонстрации точности разных алгоритмов, на рисунке приведены результаты интегрирования модуля синусоидального сигнала с частотой 0,2 Гц. Результат операции - оценочная область под серией кривых.
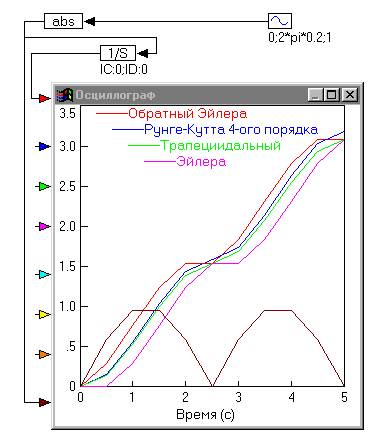
Наглядно видно, что ошибки алгоритмов интегрирования несущественны для этого примера, однако более драматические последствия могут наблюдаться в блок-схемах, содержащих дифференциальные уравнения.
Хорошее правило выбора метода интегрирования состоит в том, чтобы использовать наименее сложный алгоритм, который обеспечивает устойчивые и правильные результаты. Чтобы следовать ему можно, первый запуск модели выполнить с более сложным алгоритмом, а за тем, последовательно перебрать более простые, используя в качестве критерия заметные глазу изменения в результатах. Тот же критерий можно использовать при увеличении шага симуляции.
Если Вы планируете использовать один из алгоритмов чаще других, рекомендуется назначить его по умолчанию
Установки на вкладке 'Методы интегрирования'
Для назначения метода интегрирования выполните действия:
Выберите команду меню Симуляция > Настройки симуляции.
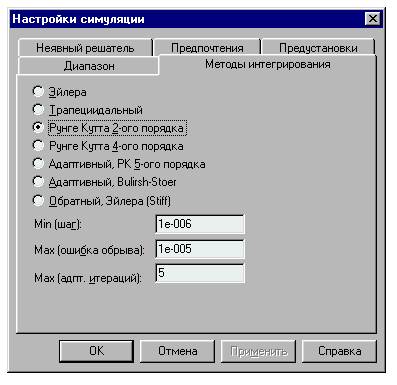
В диалоговом окне "Настройки симуляции" выберите вкладку "Методы интегрирования".
Выберите метод и (при необходимости) задайте параметры.
Нажмите на кнопку OK или клавишу ENTER.
| Метод интегрирования Описание |
| Эйлера Оценка значения выполняется один раз за шаг симуляции. На этот метод меньше всего воздействуют особенности. Он наиболее быстрый при оптимальном размере шага |
| Трапециидальный Оценка значения выполняется два раза за шаг симуляции |
| Рунге-Кутта 2-ого порядка Имеет точность второго порядка. Метод рассчитывает производную в середине шага, для оценки значения интеграла в конечной точке шага |
| Рунге-Кутта 4-ого порядка Имеет точность четвертого порядка. Метод рассчитывает производную четыре раза на каждом шаге: в начальной точке, дважды в середине шага и в конце шага. Результаты используются для оценки значения интеграла |
| Адаптивный Рунге-Кутта 5-ого порядка Имеет точность пятого порядка. Адаптивность метода проявляется в том, что при ускорении изменений (увеличении приращений) входных координат алгоритм автоматически уменьшает размер шага |
| Адаптивный Булирша-Стоера Метод использует полиномиальную экстраполяцию для оценки значения интеграла в конечной точке шага, на основе серии предыдущих значений. Алгоритм обладает малой погрешностью для гладких функций (в типовых режимах движения, когда координаты меняются с постоянной скоростью, ускорением или приращением ускорения) |
| Обратный Эйлера (жесткий) Метод наиболее эффективен для симуляции систем с большой разницей частот собственных колебаний. Другие алгоритмы требовали бы установки существенно меньшего размера шага для стабильной симуляции |
| Min (шаг) Адаптивные алгоритмы (Рунге-Кутта 5-ого порядка и Булирша-Стоера) могут менять величину шага симуляции. Размер шага непрерывно корректируется, чтобы попасть в допуск ошибки за ограниченное количество итераций. Вы можете задать его минимальный размер. Таким образом, неточные результаты могут быть получены если: минимальный размер шага слишком большой, допуск ошибки мал, или мало количество итераций. Значение по умолчанию - 1e-006 |
| Max (ошибка обрыва) При выборе адаптивных методов интегрирования, Вы должны задать максимальную ошибку между результатами двух последовательных итераций. VisSim использует ошибку обрыва для определения размера шага. Чем больше допуск ошибки, тем больший размер шага возможен. Значение по умолчанию - 1e-005 |
| Max (адапт. итераций) При выборе адаптивных методов интегрирования, Вы должны задать алгоритму максимальное количество попыток (итераций) изменения величины шага симуляции в целях уменьшения ошибки обрыва. Значение по умолчанию - 5 |
Дата добавления: 2015-08-14; просмотров: 1165;
