Математическое моделирование проточной части

Математическая модель проточной части заключается в описании газодинамических процессов и может быть использована для 1, 2-х и 3-х вальных турбин.

Исходные данные:

1) Схема турбины

2) Число каскадов

3) Число ступеней в каскаде

4) Параметры, поступающие из модели ГТД

а) мощность турбины N_т

б) расход газа на вход в 1-ю ступень G_гI

в) частота вращения n

г) давление на входе в 1-ю ступень P_o^*

д) температура газа на входе в 1-ю ступень T_o^*

е) давление воздуха P_в^*

ж) температура воздуха Т_в^*

з) относительный расход до и после горлового сечения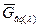

Управляющие параметры:

1. Геометрические параметры венцов

а) диаметры

б) высоты лопаток

в) хорды лопаток

г) максимальный шаг решёток

д) длины среднй линии

е) масимальные площади проходных сечений

2. Число лопаток

3. Углы натекания потоков

4. Угол установки лопатки g

5. Приведённые скорости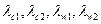

6. КПД турбины

7. Ориентировочная масса турбины

Рабочие процессы в турбине описываются уравнениями:

1. Уравнение неразрывности для сечения в осевом зазоре

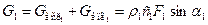
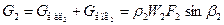
2. Уравнение энергии вдоль линии тока

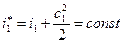
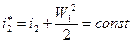
3. Уравнение смещения потока с охлаждающим воздухом

4. Уравнение процесса калорически совершенного газа

5. Уравнение состояния

6. Уравнение Эйлера

Дополняют математическую модель эмпирические и статические зависимости коэффициентов потерь: кромочных, профильных, на трение и т.д., а также зависимости геометрических параметров турбины от термогазодинамических.

Блок-схема модели приведена на рисунке:

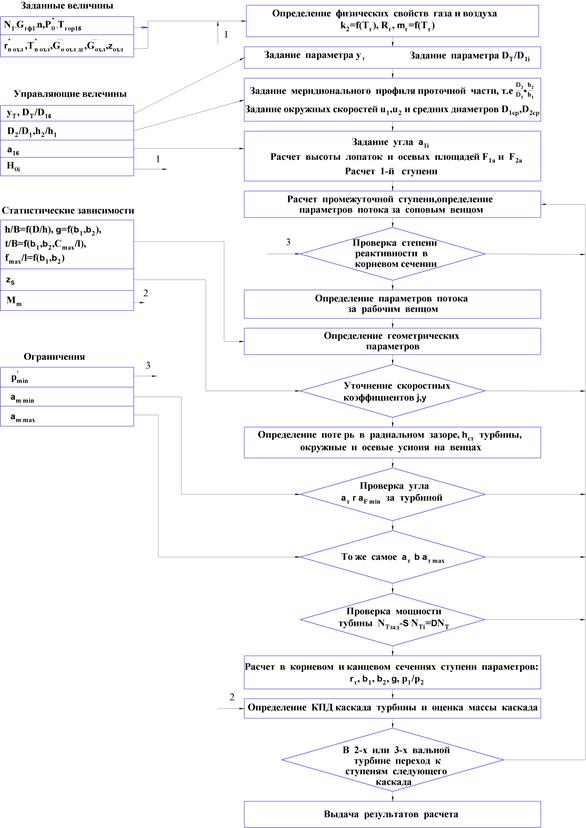
Все современные турбины полноразмерных ГТД выполняются охлаждаемыми. В настоящее время существует большое число конструктивных схем систем охлаждения. Их выбор и расчет достаточно сложен. Автоматизацию проектирования системы охлаждения обеспечивает специальная математическая модель.