Метод замены переменной в неопределенном интеграле.

Если независимую переменную х интегрирования заменить некоторой функцией и(х), дифференцируемой по х, то формула интегрирования не изменится. Во многих случаях введение новой переменной позволяет упростить подынтегральное выражение и свести интеграл к одному или нескольким табличным.

Пример 1.

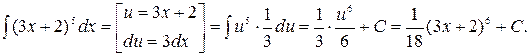
При линейной замене переменных u=ax+b интеграл сводится к табличному введением уравнивающего множителя .

Пример 2.

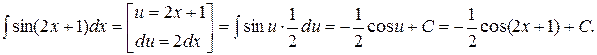
Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала.

Пример 3.

,

.

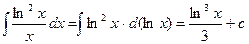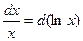Пример 4.

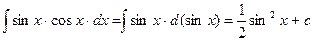, т.к. d (sin x) = cos х dx.