Линия без потерь
Линией без потерь называется линия, у которой первичные параметры 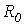 и
и 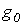 равны нулю. В этом случае, как было показано ранее,
равны нулю. В этом случае, как было показано ранее, 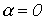 и
и 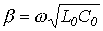 . Таким образом,
. Таким образом,
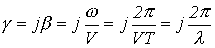 ,
,
откуда 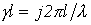 .
.
Раскроем гиперболические функции от комплексного аргумента 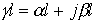 :
:
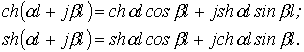
Тогда для линии без потерь, т.е. при 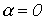 , имеют место соотношения:
, имеют место соотношения:
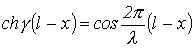 и
и 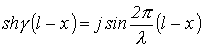 .
.
Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
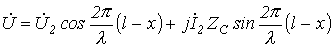 ; ;
| (17) |
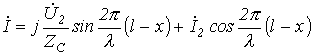 . .
| (18) |
Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении 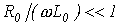 и
и 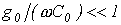 , что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
, что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
Дата добавления: 2015-08-14; просмотров: 824;
