Метод гармонического баланса
Применение аналитического выражения для аппроксимации характеристики нелинейного элемента позволяет наименее трудоемко провести расчет, когда закон изменения во времени одной из переменных, определяющих работу нелинейного элемента (ток или напряжение для резистора, потокосцепление или ток для катушки индуктивности, заряд или напряжение для конденсатора), задан или вытекает из предварительного анализа физических условий протекания процесса, что имело место при решении предыдущих задач данного раздела. Если такая определенность отсутствует, то задачу в общем случае можно решить только приближенно. Одним из таких методов, наиболее широко применимым на практике, является метод гармонического баланса.
Метод основан на разложении периодических функций в ряд Фурье. В общем случае искомые переменные в нелинейной электрической цепи несинусоидальны и содержат бесконечный спектр гармоник. Ожидаемое решение можно представить в виде суммы основной и нескольких высших гармоник, у которых неизвестными являются амплитуды и начальные фазы. Подставляя эту сумму в нелинейное дифференциальное уравнение, записанное для искомой величины, и приравнивая в полученном выражении коэффициенты перед гармониками (синусоидальными и косинусоидальными функциями) одинаковых частот в его левой и правой частях, приходим к системе из 2n алгебраических уравнений, где n-количество учтенных гармоник. Необходимо отметить, что точное решение требует учета бесконечного числа гармоник, что невозможно осуществить практически. В результате ограничения числа рассматриваемых гармоник точный баланс нарушается, и решение становится приближенным.
Методика расчета нелинейной цепи данным способом включает в себя в общем случае следующие основные этапы:
1. Записываются уравнения состояния цепи для мгновенных значений.
2. Выбирается выражение аналитической аппроксимации заданной нелинейности.
3. На основе предварительного анализа цепи и нелинейной характеристики задается выражение искомой величины в виде конечного ряда гармоник с неизвестными на этом этапе амплитудами 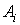 и начальными фазами
и начальными фазами 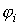 .
.
4. Осуществляется подстановка функций, определенных в пунктах 2 и 3, в уравнения состояния с последующей реализацией необходимых тригонометрических преобразований для выделения синусных и косинусных составляющих гармоник.
5. Производится группировка членов в полученных уравнениях по отдельным гармоникам, и на основании приравнивания коэффициентов при однопорядковых гармониках в их левых и правых частях (в отдельности для синусных и косинусных составляющих) записывается система нелинейных алгебраических (или трансцендентных) уравнений относительно искомых амплитуд 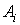 и начальных фаз
и начальных фаз 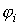 функции разложения определяемой величины.
функции разложения определяемой величины.
6. Осуществляется решение (в общем случае численными методами на ЭВМ) полученной системы уравнений относительно 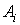 и
и 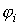 .
.
Частным случаем метода гармонического баланса являетсяметод расчета по первым гармоникам несинусоидальных величин (метод гармонической линеаризации), когда высшими гармониками искомых переменных, а также входных воздействий пренебрегают. При анализе используется характеристика нелинейного элемента по первым гармоникам, для получения которой в аналитическое выражение нелинейной характеристики для мгновенных значений подставляется первая гармоника одной из двух переменных, определяющих эту характеристику, и находится нелинейная связь между амплитудами первых гармоник этих переменных. Этапы расчета соответствуют изложенным для метода гармонического баланса. При этом, в силу того, что конечная система нелинейных уравнений имеет второй порядок, в ряде случаев появляется возможность их аналитического решения. Кроме того, поскольку рассматриваются только первые гармоники несинусоидальных величин, при расчете можно использовать символический метод.
Пусть, например, в цепи, питаемой от источника синусоидального напряжения 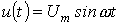 и состоящей из последовательно соединенных линейного резистора
и состоящей из последовательно соединенных линейного резистора 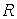 и нелинейной катушки, вебер-амперная характеристика которой задана аппроксимацией вида
и нелинейной катушки, вебер-амперная характеристика которой задана аппроксимацией вида 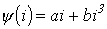 , необходимо определить первую гармонику тока, задаваемую выражением
, необходимо определить первую гармонику тока, задаваемую выражением 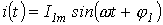 , где
, где 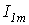 и
и 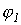 - неизвестные (искомые величины).
- неизвестные (искомые величины).
Для решения определяем аналитическое выражение характеристики 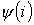 для первых гармоник:
для первых гармоник:
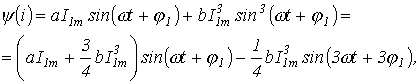
откуда
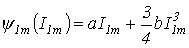 . .
| (2) |
После подстановки выражения тока и соотношения (2) в уравнение состояния цепи
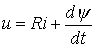
получаем
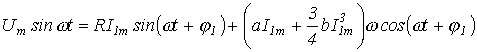
или
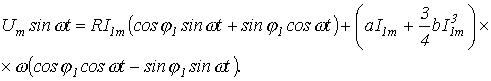
На основании последнего получаем систему уравнений
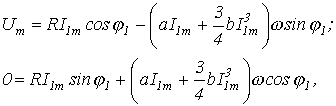
из которых находим искомые параметры 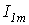 и
и 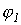 .
.
Литература
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Каплянский А.Е. и др.Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. –448 с.
Контрольные вопросы и задачи
- В чем заключается сущность метода кусочно-линейной аппроксимации?
- На чем основан метод гармонического баланса?
- Сформулируйте основные этапы расчета нелинейной цепи методом гармонического баланса.
- В чем состоит сущность метода расчета по первым гармоническим?
- Как определяется характеристика нелинейного элемента для первых гармоник?
- Резистивная нагрузка подключена к источнику синусоидального напряжения через последовательно включенный с ней диод. Считая ВАХ диода идеальной, определить коэффициент мощности. Обоснуйте физически полученный результат.
Ответ: 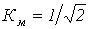 .
.
- Последовательно соединенные линейный конденсатор с
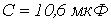 и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением
и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением 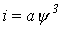 , где
, где 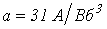 , питаются от источника синусоидального напряжения
, питаются от источника синусоидального напряжения 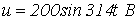 . Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
. Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
Ответ: 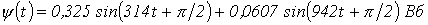 .
.
Дата добавления: 2015-08-14; просмотров: 570;
