Сполука 4.

Структурну формулу сполуки можна розбити на 4 ізольовані фрагменти:

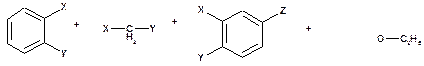
У спектрі повинно спостерігатися накладання сигналів цих структурних фрагментів. В наведеній вище таблиці містяться три з них (відповідно рядки 18, 20 та 2). Якщо в спектрі сполуки знайти сигнали, що за формою мультиплетів близькі до тих, що наведені у таблиці, то можна ідентифікувати основну кількість сигналів. При цьому віднесення синглету метиленової групи, що міститься в спектрі на додаток до них, не становитиме проблеми. При порівнянні спектру з табличними даними завжди слід пам’ятати, що можливі відхилення в положеннях сигналів від табличних величин, які зумовлені наявністю електронодонорних чи електроноакцепторних замісників. Тому на першому етапі аналізу спектру слід звернути увагу лише на форму мультиплетів, а вже потім проаналізувати, чи наявні в молекулі структурні особливості узгоджуються з відхиленнями хімічних зсувів від табличних даних. Слід зауважити, що така інтерпретація спектру є простою лише в тому випадку, коли сигнали одних структурних фрагментів не співпадають повністю з сигналами інших фрагментів. Якщо наявні перекривання сигналів, то вигляд спектру може докорінно змінитися – замість чітких піків з видимою мультиплетністю в спектрі можуть з’явитися складні сигнали невизначеної форми, які мають інтегральну інтенсивність в декілька протонів. Особливості інтерпретації таких складних спектрів будуть пояснені у наведених нижче прикладах, де розібрано декілька варіантів аналізу спектрів, що є найбільш поширеними.

2.10. Аналіз спектру чистої сполуки

Вимірювання та аналіз спектрів на ядрах ¹Нє ЯМР дослідженням, що проводиться найчастіше. Синтез нових сполук, їх виділення з реакційної суміші та очистка різними методами потребують контролю за допомогою ЯМР. Цей контроль полягає в аналізі вигляду спектру з метою ідентифікації сигналів домішок та встановленні відповідності спектру передбачуваній структурі сполуки. Для проведення аналізу часто буває достатнім виміряти оглядовий спектр ЯМР. Головна вимога до такого спектру – запис його у масштабі, що є достатнім для аналізу мультиплетності сигналів. Крім того, спектр повинен містити інтегральну криву та цифрові дані про хімічні зсуви сполуки. Типовим спектром, що придатний для ідентифікації сполуки, є спектр, що наведений на Рис. 12.

Спектр містить фрагменти сигналів ароматичних протонів у збільшеному масштабі для більш точного аналізу їхньої мультиплетності.

Аналіз спектру слід розпочинати з розгляду передбачуваної формули сполуки. В ній треба виділити окремі фрагменти, що утворюють ізольовані спінові системи та якомога точніше передбачити (використовуючи довідкові дані), як будуть виглядати їхні сигнали в спектрі. У нашому прикладі маємо 5 ізольованих спінових систем:

а) протони метильної групи (інтенсивність сигналувідповідає трьом протонам, що позначається як 3Н) повинні відповідати спіновій системі А₃. Оскільки ця група містить три еквівалентних протони, що не мають спінового зв’язку з іншими ядрами, то її сигнал повинен бути синглетом;

б) протон NН групи (інтенсивність сигналу1Н). Розташований в молекулі таким чином, що від найближчого протона його відділяють 4 хімічних зв’язки. Тому він являє собою спінову систему А₁ і його сигнал також повинен бути синглетом;

в) протони піран-2-онового циклу (три сигнали по 1Н кожний), згідно з формулою, утворюють систему АВХ. При цьому один з сигналів, що відповідає протону, який розташований поблизу гетероциклічного атому кисню, повинен міститися у значно більш слабкому полі, ніж сигнали двох інших протонів, що відповідають метиленовій групі. Типовий вигляд спектру цього фрагменту міститься у таблиці, що наведена вище (рядок 5);

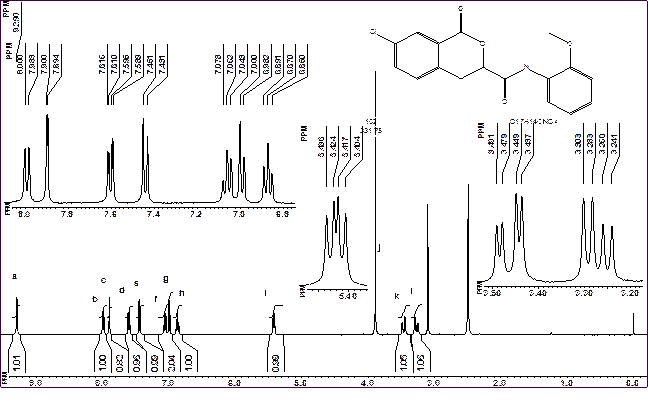
Рис. 12. Спектр ЯМР на ядрах ¹Н, придатний для ідентифікації сигналів

г) протони ароматичного циклу бензопірону (три сигнали по 1Н) відповідають спіновій системі АМХ. Вони повинні розташовуватися в діапазоні 6-8 м.ч. Передбачити мультиплетність цих сигналів можна з аналізу того, скільки протонів розташовано на відстані 3 хімічних зв’язків від кожного з протонів. Згідно з формулою, два з числа протонів даної спінової системи є віцинальними (вони віддалені один від одного на 3 хімічних зв’язки), а третій протон – більш ізольований. Від нього до найближчого протона 4 зв’язки. Таким чином, для даної спінової системи можна очікувати появу синглету та двох дублетів. Однак, слід пам’ятати, що в ароматичних системах спін-спіновий зв’язок може передаватися і через 4 хімічних зв’язки. КССВ при цьому може становити 2-3 Гц. Тому синглет та один з дублетів спінової системи, що розглядається, може бути розщеплений з невеликою КССВ. Типовий вигляд спектру цього фрагменту міститься у таблиці, що наведена вище (рядок 20);

д) протони ароматичного циклу анілінового фрагменту відповідають спіновій системі АMQX, вони дають сигнали з сумарною інтенсивністю 4Н. З огляду на кількість протонів, що віддалені один від одного на 3 хімічних зв’язки, для сигналів даної системи слід очікувати появи в спектрі двох дублетів та двох триплетів (можливе також подальше розщеплення компонентів цих сигналів завдяки ССВ через 4 зв’язки). Сигнали повинні розташовуватися в діапазоні 6-8 м.ч. Типовий вигляд спектру цього фрагменту міститься у таблиці, що наведена вище (рядок 18).

Тепер, коли ми, виходячи з формули сполуки, вже передбачили, які саме сигнали повинен містити спектр, треба знайти їх у наведеному спектрі. Перш за все, звернімо увагу на інтегральні інтенсивності сигналів. Вони позначені під відповідними сигналами (деякі програми обробки спектрів позначають їх також над сигналом чи біля інтегральної кривої). Бачимо, що лише один з сигналів має інтенсивність 3Н (сигнал j). Він розташований при 3,85 м.ч. і відповідає метоксильній групі. Синглет при 9,38 м.ч. знаходиться в області, що нехарактерна для поглинання ароматичних протонів. Тому його слід віднести до протону NН. Слід запам’ятати, що протони NН та ОН можуть розташовуватися в дуже широкому спектральному діапазоні (1-16 м.ч.). Тому, якщо в спектрі містяться сигнали з незвичайними хімічними зсувами, то часто вони належать саме таким протонам (їх називають рухливими). Довести приналежність сигналу до груп NН та ОН можна за допомогою дейтерообміну, що відбувається при додаванні до розчину краплини дейтерованої води. Якщо за цих умов повторно виміряти спектр, сигнали рухливих протонів зникнуть, чи зменшать свою інтенсивність.

Кількість протонів в ароматичній області (6.7-8.0 м.ч.) відповідає наведеній формулі. Слід лише віднести сигнали до спінових систем, що містяться в молекулі. В нашому випадку сигнали c, d, e відповідають ароматичним протонам анельованого до гетероциклу бензольного кільця (А), а сигнали b, f, g, h відповідають протонам анілінового циклу (Б). При віднесенні сигналів слід уважно аналізувати їхню мультиплетність та викривлення інтенсивності (ефект даху). Так, приналежність сигналів d та е саме протонам кільця А витікає, з одного боку, з наявності далекої КССВ з протоном с, а, з другого боку, з однакового збільшення інтенсивності внутрішніх компонентів мультиплетів, що свідчить про наявність спінового зв’язку між ними.

Сигнали протонів 2-піронового фрагменту дають в спектрі три дублети дублетів (сигнали і, k, l). Вигляд сигналів є характерним для системи АВХ, де всі КССВ є неоднаковими. Окрім сигналів сполуки, в спектрі міститься сигнал розчинника – ДМСО-D₅ при 2,5 м.ч., а також сигнал води при 3,2 м.ч. Таким чином, спектр сполуки повністю відповідає її формулі.

2.11. Аналіз спектру сполуки, що містить домішки

Розглянемо приклад спектру, що окрім сигналів цільової сполуки, містить також і сигнали домішок. Такі спектри можна отримати у випадку, якщо сполука після синтезу не була додатково очищена. Хоча будова домішок може бути різною, але найчастіше домішками є або вихідні речовини, або розчинники, або продукти альтернативних реакцій. Аналіз спектру може дати хіміку цінні відомості про присутність у зразку речовин, що, хоч і не є цільовими, але вони є продуктами конкуруючих процесів. Вони можуть бути навіть більш цікавими, ніж основна реакція. Тому, коли Ви отримали спектр брудної речовини, проаналізуйте вигляд сигналів домішок. Якщо ж спектр містить сигнали розчинників, то не слід додатково очищувати сполуку, достатньо її добре висушити.

Нижче на рисунку наведено спектр сполуки, що є близьким аналогом попередньої. Як і раніше, перш за все встановимо відповідність сполуки наведеній формулі, для чого проаналізуємо, сигнали яких спінових систем повинні міститися в спектрі, виходячи з будови сполуки.

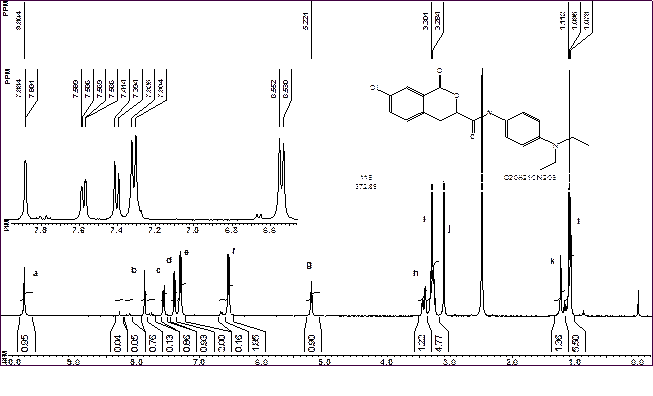
Рис. 13. Спектр ¹Н сполуки, що має домішки

Сполука містить дві еквівалентні етильні групи (рядок 2 у табл. 6). Тому в спектрі слід очікувати появи триплету та квартету з відносними інтенсивностями сигналів 4Н та 6Н відповідно. В слабкому полі повинен міститися синглет NH. Протони бензопіран-2-онового кільця повинні дати в ароматичній області сигнали спінової системи АМХ, а саме - два дублети та синглет з можливим подальшим розщепленням завдяки дальнім КССВ (рядок 20 у табл. 6). Ароматичні протони анілінового фрагменту утворюють спінову систему АА’BB’, що у більшості випадків має вигляд двох дублетів з відносною інтенсивністю 2Н кожний (рядок 16 у табл. 6). Протони піран-2-онового циклу утворюють систему АВХ з неоднаковими КССВ між кожним з протонів (рядок 5 у табл. 6). Таким чином, їх сигнали повинні мати вигляд трьох дублетів дублетів.

Аналіз спектру дозволяє виявити в ньому всі спінові системи, що відповідають формулі сполуки. Так, сигнал а відповідає протону NH. Сигнали b, c, d, що мають вигляд двох дублетів та синглету з відносною інтенсивністю 1Н кожний, є сигналами ароматичних протонів циклу А. Два дублети e та f інтенсивністю по 2Н пов’язані з ароматичними протонами анілінового фрагменту. В найбільш сильному полі, при 1,38 м.ч. видно триплет, а при 3,28 м.ч. – квартет етильної групи. Є в спектрі і сигнали спінової системи АВХ 2-оксопіранового циклу. Але в даному випадку один з сигналів співпадає з сигналом метиленових протонів етилу. Це видно з його завищеної інтегральної інтенсивності. Сигнал при 3,28 м.ч. має відносну інтенсивність не 4Н, а 5Н. Інші два сигнали спінової системи АВХ спостерігаються окремо (сигнали g та h). Таким чином, спектр сполуки відповідає наведеній формулі. Але окрім сигналів, інтенсивність яких відповідає одному чи кільком протонам, в спектрі міститься ряд сигналів порівняно низької інтенсивності. Їх добре видно при збільшенні масштабу ароматичної області спектру. Є сторонній сигнал також і в аліфатичній області (сигнал при 1,24 м.ч.). Таким чином, спектр містить сигнали домішок. Для того, щоб оцінити їхню кількість, вважають, що молекулярна маса домішки не сильно відрізняється від молекулярної маси основної сполуки. У цьому випадку в першому наближенні співвідношення інтенсивностей сигналів основної сполуки та домішок приблизно відповідає мольній долі домішки. Так, якщо вважати, що сигнал домішки при 6,65 м.ч. відповідає двом протонам, аналогічним двом протонам основної речовини, що поглинають при 6,54 м.ч., то вміст домішки дорівнює 0,17/(2 + 0,17) = 8(мольних)%. Слід ще раз зауважити, що розрахований таким чином вміст домішок є дуже приблизним, оскільки насправді невідома не лише хімічна будова і молекулярна маса домішки, а навіть кількість домішкових компонентів. Але серед хіміків усталеним є підхід: якщо сигнали кожного з протонів домішок не перевищують за інтенсивністю 0,1Н, то сполука вважається достатньо чистою для подальшої роботи та біологічних досліджень. У такому разі за найгірших умов вміст домішки не перевищує 10%, а насправді, коли домішкою є один з вихідних компонентів, він становить близько 5%.

2.12. Аналіз складних спектрів ПМР

У попередніх параграфах були розглянуті досить прості спектри, що не містили сигналів, які перекриваються. При аналізі спектрів часто доводиться стикатися з ситуацією, коли в спектрі видно не окремі сигнали, а погано структуровані мультиплети, що є результатом накладання декількох сигналів. Форма сигналів при цьому здебільшого є такою, що неможливо заздалегідь передбачити, які саме сигнали утворили цей складний мультиплет. Аналіз таких спектрів щодо їх відповідності передбачуваній структурі має деякі особливості. Перш за все, слід проаналізувати значення інтегральних інтенсивностей окремих сигналів і впевнитися, що загальна кількість протонів відповідає структурній формулі молекули. При цьому треба особливу увагу приділити інтенсивності складних сигналів. Оскільки як стандарт інтенсивності береться той сигнал, кількість протонів в якому є відомою, то величини інтегралів інших сигналів, що містяться у спектрі, є похідними від цієї величини. Слід мати на увазі, що значення інтегральних інтенсивностеє не є точними, вони вимірюються з деякою, іноді значною (5-10%) похибкою. Якщо, як це було раніше, всі сигнали спостерігалися окремо, то відхилення їхніх величин інтегралів не перевищували декількох відсотків. Якщо ж є сигнал, що відповідає одночасно 4-5 протонам, то для нього інтегральна інтенсивність може становити, наприклад, 4,5Н. У такому випадку може здатися, що в цілому спектр містить на 1 протон більше, ніж це відповідає формулі, або менше, ніж це передбачається. У такому випадку на першій стадії аналізу спектру доцільно вважати, що він узгоджується зі структурою і шукати ґрунтовні аргументи, що можуть похитнути таку думку. За аналогією з юриспруденцією, такий підхід можна назвати презумпцією відповідності. Тому, якщо значення інтегральної інтенсивності складного сигналу не є цілим числом, можна спробувати присвоїти йому потрібне значення (виходячи зі структури молекули) і подивитись, як зміняться при цьому інтенсивності інших сигналів. Якщо їх величини відхиляються від цілих чисел не більше ніж на 0,1Н, то вважають, що інтеграл узгоджується зі структурною формулою. Якщо це не зовсім так, як репер інтенсивності можна вибрати довільний сигнал, що присутній у спектрі. Якщо при хоч одному варіанті вибору реперу, всі інтеграли близькі до цілих величин, можна вважати, що сполука має передбачувану кількість протонів. Нижче наведено фрагмент спектра, для якого спостерігається саме така ситуація:

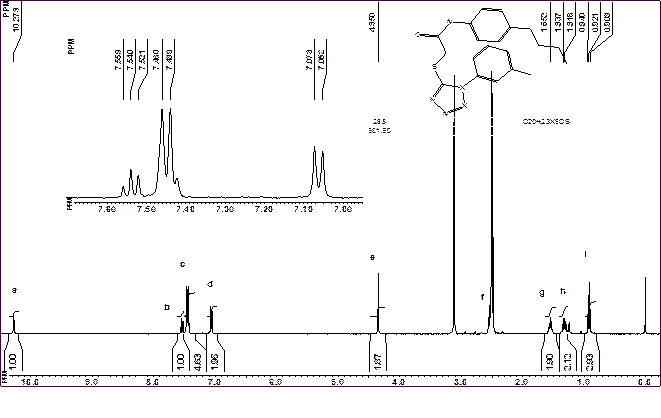
Рис. 14. Спектр ¹Н сполуки з сигналами, що співпадають і недосконало встановленими інтегральними інтенсивностями сигналів

Бачимо, що сигнал с, який є результатом накладання декількох сигналів, має неціле значення інтегральної інтенсивності, що не дозволяє надійно проаналізувати спектр. При цьому інтенсивності всіх інших сигналів досить близькі до цілих величин. З формули видно, що сполука повинна містити 8 ароматичних протонів, тому сигнал с повинен складатися з п’яти протонів. Нижче (Рис. 15) наведено той самий спектр сполуки, але як репер інтегральної інтенсивності взято сигнал метиленових протонів g, причому йому присвоєне значення 2Н.

Бачимо, що в даному випадку всі інтенсивності достатньо близькі до цілих величин. Те, що відносні інтегральні інтенсивності залежать від вибору репера, обумовлено, з одного боку, неточностями інтегрування, а, з другого боку – ефектами насичення, які завжди можуть мати місце в спектрі. Якщо як репер інтенсивності вибрати сигнал ядер, що повністю не відрелаксували, який має занижену інтенсивність, то всі інші сигнали матимуть завищену інтенсивність.

Після того, як Ви впевнились, що сполука має потрібну кількість протонів, слід переходити до аналізу мультиплетності сигналів. Якщо всі сигнали в спектрі, що спостерігаються окремо, можна віднести до конкретних протонів, що містяться у молекулі, то можна вважати, що всі не віднесені сигнали накладаються один на одний і дають складний мультиплет. У таких випадках вважається, що сполука відповідає передбачуваній структурній формулі за умов, коли вивчається не одна сполука, я ряд структурних аналогів, що мають деякі відмінності у структурі. В таких рядах практично завжди хоч для однієї з сполук спектр виявляється достатньо простим для повного віднесення сигналів. Якщо ж досліджувана сполука є єдиною, то для більшої певності у віднесенні сигналів слід виміряти її спектр на ядрах ¹³С, чи провести інші додаткові ЯМР експерименти. В нашому прикладі до складу сигналу с з інтенсивністю 5Н попадають два дублети та синглет фрагменту, що є м‑заміщеним фенілом та один з двох протонних дублетів фрагменту п‑фенілу. Всі інші сигнали, що є у спектрі, узгоджуються з формулою. Так, сигнал а при 10,5 м.ч. відповідає протону NH, триплет b відповідає протону Н5 м-фенілу, дублет d інтенсивністю 2Н пов’язаний з протонами п-фенільного замісника, синглет е відповідає ізольованій метиленовій групі, а сигнали f-і відповідають протонам бутильного замісника. Наведений приклад ілюструє те, що спектр ЯМРне є 100%-ною гарантією того, що цільова сполука має передбачувану будову. Для більшої певності слід вимірювати спектр речовини також і на інших ядрах, частіше за все на ядрах ¹³С. Коли і цей спектр узгоджується зі структурою молекули, то вірогідність правильних висновків про структуру збільшується.

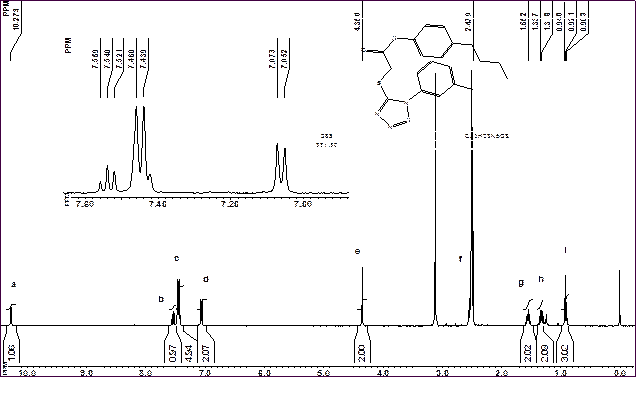
Рис. 15. Спектр ¹Н сполуки зі співпадаючими сигналами при правильному встановленні інтегралів

2.13. Залежність величини КССВ ядер ¹Н від будови хімічних сполук

КССВ відображають ефективність переносу інформації про орієнтацію спіна одного з магнітних ядер (чи групи ядер) на інші магнітні ядра. Оскільки цей процес відбувається за участю електронів, що утворюють хімічні зв’язки, то величини КССВ відображають певні властивості цих зв’язків, зокрема їх кратність та взаємну орієнтацію у просторі. Тому, якщо виміряні КССВ та відома структура досліджуваної молекули, можна робити висновки про її просторову будову. Внаслідок цього аналіз КССВ є поширеним методом конформаційного аналізу органічних сполук. Особливою перевагою методу є те, що він не потребує додаткових досліджень – достатньо просто виміряти необхідні КССВ та провести відповідні розрахунки. Після цього можна моделювати структурний фрагмент молекули, що містить ядра зі знайденими КССВ. У протонній спектроскопії існує ряд емпіричних зако­номірностей, що зв'язують величини КССВ з будовою молекул. За їхньої допомоги можна передбачити, якими будуть КССВ для тієї чи іншої хімічної сполуки.

2.13.1. Гемінальні КССВ

Це константи ²J_HH. Вони найчастіше трапляються у фрагменті СН₂ і мають величини в інтервалі від -23 Гц у молекулі циклопентадієну до +41 Гц у молекулі формальдегіду. Як бачимо, діапазон даних КССВ є досить великим, причому може змінюватися не тільки видима абсолютна величина ²J_HH, а й її знак. При порівнянні сполук може трапитися ситуація, коли більша гемінальна КССВ є меншою за видим значенням. Так, наприклад, збільшення ²J_HH в ряду сполук від -10 Гц до +2 Гц візуально сприйматиметься як зменшення величини даної КССВ на 8 Гц. В цілому великі негативні значення гемінальних КССВ є більш характерними, тому, якщо у спектрі сполуки спостерігається велика гемінальна КССВ, то з високою вірогідністю вона має негативний знак. Коли ж гемінальна КССВ є невеликою, то вона може бути як позитивною, так і негативною. Нижче, на рис. 16, наведено типові значення гемінальних КССВ для органічних сполукрізноманітної будови.

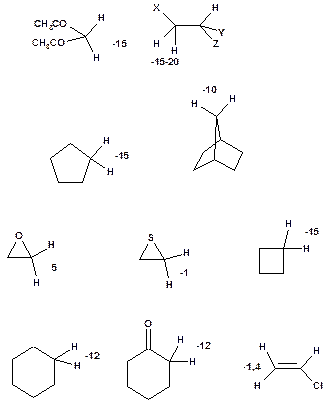
Рис. 16. Залежність величини гемінальної КССВ від будови молекули

Тут здебільшого наведено величини ²J_HH для незаміщених сполук. Наявність електроноакцепторних замісників поруч з метиленовою групою зменшує КССВ на 3-5 Гц (якщо КССВ негативна, абсолютна її величина збільшується). Найчастіше з гемінальними КССВ доводиться мати справу, коли вимірюються спектри циклічних сполук, або коли в сполуці міститься метиленова група у фрагменті, що не здатний вільно обертатися. Гемінальна КССВ може також проявлятися між протонами метиленових груп в хіральних сполуках, навіть коли можливе вільне обертання відповідних фрагментів. У таких випадках протони метиленових груп є діастереотопними, що зумовлює неоднакові хімічні зсуви їхніх сигналів. У випадку, коли можливий ефективний перехід між конформерами в ахіральних сполуках, хімічні зсуви протонів метиленової групи усереднюються і, відповідно, вони дають у спектрі синглет.

2.13.2. Віцинальні КССВ

Константи, що відповідають спін-спіновій взаємодії ядер через три хімічні зв’язки, називають віцинальними. З ними доводиться мати справу найбільш часто. Величини констант ³J_НН спостерігаються у діапазоні від 0 до 20 Гц. Знак віцинальних КССВ, як правило, позитивний. Вони зустрічаються у сполуках практично всіх типів – в ароматичних, гетероциклічних, аліциклічних та аліфатичних. Оскільки спін-спінова взаємодія через три хімічні зв’язки передається досить ефективно, то віцинальні КССВ порівняно великі. На них впливають як електронні, так і стереохімічні особливості молекули, тому віцинальні КССВ часто використовуються для знаходження просторової будови органічних сполук. Для аліфатичних сполук, як це було показано Карплусом, вони залежать від величини двогранного кута θ між площинами, в яких лежать зв'язки С—Н. Графік цієї залежності показано на рис. 17.

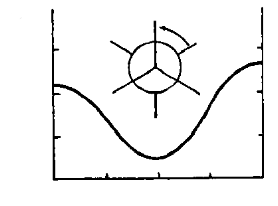
Рис. 17. Залежність віцинальної КССВ від торсійного кута у фрагменті Н‑С-С-Н

Як видно з графіку, в залежності від взаємної орієнтації протонів, величини віцинальних КССВ можуть знаходитися в діапазоні від 3 до 14 Гц. Аналітично залежність віцинальної КССВ від торсійного кута у фрагменті Н-С-С-Н у найпростішому випадку виражається рівнянням, яке ще називають формулою Карплуса:

³J_HH = A + Bcosj + Ccos 2j

Рівняння містить три емпі­ричні параметри: А, В та С. Значення цих параметрів значною мірою залежать від наявності в молекулах електроноакцепторних замісни­ків, причому наявність та­ких замісників зумовлює збільшення КССВ. Для вуглеводнів А = 7 Гц, В = 1 Гц, С = 5 Гц. Згідно з даним рівнянням, вимірювання віцинальної КССВ дозволяє знайти просторову орієнтацію протонів, між якими існує віцинальна спін-спінова взаємодія. Ряд програм для ПК, де виконується оптимізація стереохімічної будови молекули методами молекулярної механіки чи квантової механіки, здатні обчислювати передбачувані віцинальні КССВ для розрахованої будови молекули. Такі обчислення, як правило, здійснюються за допомогою формули Карплуса, або її більш складних (уточнених) варіантів.

За рівнянням Карплуса можна оцінити кути між зв’язками і в циклічних сполуках. В жорстких циклах можна встановити, знаходяться протони по один бік кільця (цис-орієнтація) чи по різні боки (транс-орієнтація). У менш жорстких шестичленних циклах, де можливими є декілька конформацій, можна також знайти, які протони в є аксіальними, а які – екваторіальними. Таким чином, опосередковано можна знайти орієнтацію замісників в циклах.

В ароматичних сполуках величини віцинальних КССВ визначаються розмірами циклу та наявністю у ньому гетероатомів. Збільшення розміру циклу зумовлює збільшення величин віцинальних КССВ. Так, для п'ятичленних циклів характерними є КССВ 4-6 Гц, для 6-членних – 7,5-8,5 Гц, а для 7-членних – 10-12 Гц. Нижче, на рис. 18, наведено величини віцинальних КССВ для деяких органічних сполук.

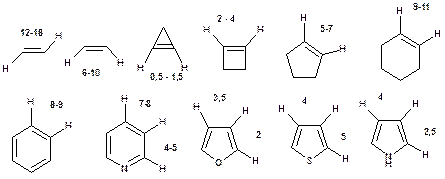
Рис. 18. Типові величини віцинальних КССВ

2.13.3. Далекі КССВ

Далекими називаються КССВ, що передаються через 4 хімічних зв’язки, або більше. Зазвичай у більшості хімічних сполук такі КССВ не спостерігаються. Але, за сприятливого взаємного розташування протонів в жорстких молекулах можна спостерігати їхню взаємодію навіть через 5 хімічних зв’язків. Такі випадки можуть траплятися як в аліфатичних, так і в ароматичних сполуках. В насичених системах ⁴J_нн мають помітні значення тільки в молекулах з жорсткою структурою у випадках, коли хімічні зв'язки, що розділяють протони, лежать в одній площині і їх конфігурація нагадує літеру W(так звана W‑взаємодія).Найбільш ефективно ССВ передається через 4 зв’язки у випадках, коли, завдяки структурним особливостям молекули, існує декілька шляхів передачі спінової інформації. Така ситуація реалізується у біциклічних сполуках, що містять малі цикли. Для них ⁴J_HH можуть сягати і 18 Гц. Нижче, на Рис. 19, наведено ряд таких сполук. В конформаційно-рухливих молекулах дальні КССВ найчастіше близькі до нуля.

Помітними є величини ⁴J_нн у ненасичених сполуках (алільні КССВ). Звичайне значення цих констант становить 1 —3 Гц.

Рис. 19. Величини далеких КССВ ¹Н-¹Н для деяких сполук

3. Спектроскопія на ядрах ¹³С

В принципі, вимірювання вуглецевих спектрів можна проводити цілком аналогічно до протонних і в результаті отримувати спектри, де сигнали мають розщеплення завдяки ССВ. Однак, ситуація ускладнюється тим, що ми вимірюємо не сигнали основного ізотопу (¹²С), а сигнали на ядрах ¹³С, причому таких ядер у природній суміші ізотопів вуглецю знаходиться всього ~1%. Тому сигнал ЯМР виявляється малоінтенсивним. Для вимірювання таких спектрів доводиться використовувати прийоми, що дозволяють збільшити інтенсивність сигналів. Для цього у більшості випадків використовуються методики гетероядерного декаплінгу, тобто додаткового опромінювання зв’язаних з атомами вуглецю магнітних ядер (найчастіше протонів, позначається як С{¹H}).

Метою гетероядерного декаплінгу є спрощення спектру і підвищення інтенсивності сигналів завдяки гетероядерному ЯЕО.

3.1. Спектри ¹³С в умовах декаплінгу на протонах С{¹H} Різновиди

Використання широкосмугового протонного декаплінгу під час накопичення вуглецевих спектрів застосовується для більшості вимірювань. Видалення всіх розщеплень ¹Н-¹³С приводить до зосередження всієї інтенсивності вуглецевих сигналів в одній лінії, що веде до значного зростання інтенсивності спектра і до його спрощення. (Зауважимо, що у випадку, коли до молекули входять, окрім протонів та ¹³С, ще інші магнітні ядра (наприклад, ¹⁹F, ³¹H) розщеплення сигналів за рахунок ССВ з цими ядрами в спектрах ¹³С{¹H} проявляються).

Ще одним „подарунком” є подальше зростання інтенсивності вуглецевих сигналів за рахунок ядерного ефекту Оверхаузера. У випадку ¹³С цей ефект може сягати 200%. Внаслідок цього використання широкосмугового протонного декаплінгу є стандартним прийомом для вимірювання рутинних вуглецевих спектрів.

Використовують три різновиди широкосмугового декаплінгу і, відповідно, існують три типи вуглецевих спектрів, що можна при цьому отримати. Для того, щоб зрозуміти їх відмінності, найпростіше скористатися зображенням відповідних імпульсних послідовностей, що для цього використовуються. Вони показані на Рис. 20. В першій з них декаплер вмикається на протязі релаксаційного проміжку, що передує подачі імпульсу на ядрах ¹³С і вимикається безпосередньо перед подачею імпульсу. При дії такого декаплінгу виникає підсилення сигналів завдяки ефекту Оверхаузера. Але, оскільки при зборі даних декаплер є вимкненим, то ССВ ¹³С-¹Н в спектрах проявляється. Отже, ми отримуємо розщеплений спектр з мультиплетами, що відповідають ССВ з протонами, але підвищеної інтенсивності. Такий різновид спектрів використовують для вимірювання гетероядерних КССВ. Він називається переривчастим декаплінгом. У другому варіанті декаплер вмикається лише на період збору даних. При цьому не проявляються всі гетероядерні КССВ С-Н, але не виникають ЯЕО. Цей різновид спектрів використовують для вимірювання інтенсивності вуглецевих сигналів. Його називають оберненим переривчастим декаплінгом. Третій різновид декаплінгу, про який вже йшла мова на початку цього розділу – це такий варіант, коли декаплер працює безперервно. Іноді на різних етапах імпульсної послідовності варіюють його потужність для запобігання нагріванню зразка. Отримані у такий спосіб вуглецеві спектри використовують найбільш часто. В них сигнали підсилені завдяки ЯЕО і відсутнє розщеплення сигналів.

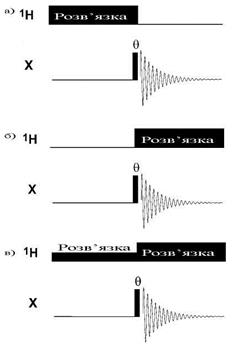
Рис. 20. Можливі схеми протонного декаплінгу при спостереженні гетероядер. (a) переривчастий декаплінг (розщеплений спектр із ЯЕО), б) обернений переривчастий декаплінг(розв'язаний спектр без ЯЕО) і в) декаплінг зі змінною потужністю (розв'язаний спектр із ЯЕО).

Застосування описаних схем декаплінгу проілюстровано на Рис. 21 на прикладі спектра a-пінену 5.

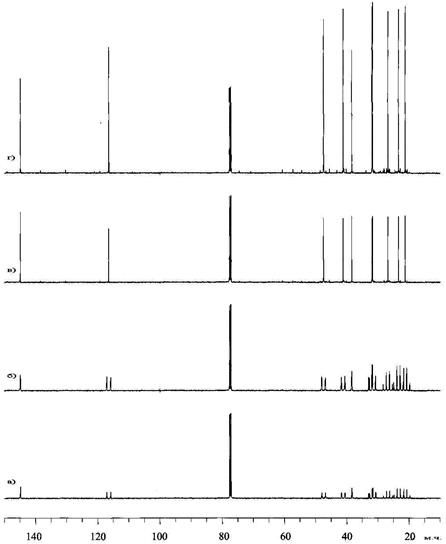
Рис.1.21 Спектр ¹³С α-пінену (5), що отриманий (a) без декаплінгу (розщеплений спектр без ЯЕО), (б) з оберненим переривчастим декаплінгом (розщеплений спектр із ЯЕО), (в) з переривчастим декаплінгом (розв’язаний спектр без ЯЕО) і (г) з декаплінгом зі змінною потужністю (розв’язаний спектр із ЯЕО). Всі інші умови експериментів, включаючи шкалу інтенсивності сигналів, були ідентичними.

3.2. Аналіз вуглецевого спектрусполуки

На відміну від оглядових протонних спектрів, вуглецеві спектри, якщо вони виміряні за стандартних умов (при дії широкосмугового декаплінгу на протонах) є менш інформативними, оскільки не містять відомостей не тільки про КССВ, а навіть про мультиплетність сигналів і їх відносну інтенсивність, а отже і про кількість протонів, що зв’язані з певними атомами вуглецю. Основна інформація, що зосереджена в таких спектрах, полягає в кількості вуглецевих атомів в молекулі, що знаходяться в різному хімічному оточенні. Оскільки діапазон хімічних зсувів атомів вуглецю є значно більшим, ніж у протонів, то співпадання сигналів є менш імовірним. Тому кількість піків у вуглецевому спектрі в багатьох випадках відповідає кількості хімічно нееквівалентних вуглецевих атомів у молекулі. Зараз значна кількість наукових журналів вимагає, щоб у матеріалах статей містилися дані вуглецевих спектрів нових сполук. В експериментальну частину статті треба вносити перелік хімічних зсувів атомів вуглецю, що отримано з оглядового вуглецевого спектру.

Розглянемо хід аналізу вуглецевого спектру на прикладі досить простої сполуки, гетероциклічного броміду 6.

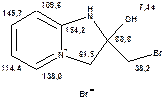
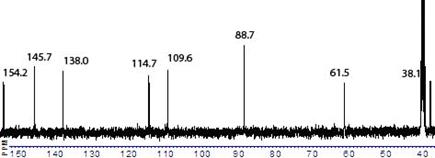
Рис. 22. Спектр ¹³С гетероциклічного броміду 6, знятий в умовах широкосмугового декаплінгу.

Зі спектра видно, що кількість синглетів в ньому відповідає кількості вуглецевих атомів в молекулі (мультиплет при ~40 м.ч. відповідає сигналу розчинника). Три з них, що мають хімічні зсуви, менші за 90 м.ч., відповідають аліфатичним атомам вуглецю. Інші п’ять сигналів дають ароматичні атоми вуглецю. На формулі сполуки наведено віднесення вуглецевих сигналів. Однак, для однозначного віднесення в спектрі не досить даних. Так, якщо аліфатичні сигнали можна віднести достовірно, оскільки відповідні їм атоми вуглецю відрізняються досить сильно, то сигнали атомів піридинового циклу віднести не вдається. Єдине, що можна стверджувати напевно, це те, що сигнал при 154,2 м.ч. відноситься до вузлового атому вуглецю. Для всіх інших сигналів можна запропонувати декілька варіантів віднесення. Так, a- та g-атоми вуглецю піридинового кільця, якщо виходити з відповідних табличних даних, можна віднести не так, як це наведено на формулі сполуки. Тому при аналізі навіть простих вуглецевих спектрів не слід без додаткових експериментів проводити остаточні віднесення сигналів. Достатньо, якщо положення наявних сигналів попадають у притаманні їм діапазони хімічних зсувів. Якщо ж віднесення сигналів є необхідним для висновків про структуру молекули, слід, окрім оглядового вуглецевого спектру, виміряти спектри DEPT, HMQC та HMBC (див. далі). Аналіз сукупності отриманих таким чином даних дозволяє у більшості випадків провести надійне віднесення сигналів. Саме так і було здійснене віднесення вуглецевих сигналів даної сполуки. Як проводяться такі дослідження, буде показано у відповідному розділі книги.

Якщо результати вимірювання вуглецевого спектру потрібні для експериментальної частини наукової праці, то для розглянутого спектру опис матиме такий вигляд:

Спектр ¹³С, в розчині ДМСО-D₆, сигнали в м.ч. відносно ТМС: 154,2; 146,7; 138,0; 114,7; 109,6; 88,8; 61,5; 38,2. Тут у дужках можна вказати віднесення сигналів, якщо воно зроблене надійно. Але на відміну від описів протонних спектрів, не вказуються відносні інтенсивності сигналів та величини КССВ, а наводиться лише перелік хімічних зсувів.

3.3. Кореляції хімічних зсувів ядер ¹³С з будовою молекул

Ядра атомів вуглецю ¹³С поглинають, як правило, у діапазоні 0—250 м. ч. відносно сигналу ТМС. Загальні закономірності залежності величин хімічних зсувів у вуглецевих спектрах від будови молекул приблизно такі ж самі, як і в про­тонних. Відрізняється лише масштаб зміни хімічних зсувів ядер ¹³С та КССВ при певних змінах будови речовини. У найсильнішому полі (0-60 м. ч.) поглинають ядра вуглецевих атомів насичених вуглеводневих радикалів. Перехід від четвертинного вуглецевого атома до третинного, вторинного і, нарешті, до первинного супро­воджується зменшенням його хімічного зсуву. Однак, діапазони зсувів, характерні для якогось одного типу вуглецевих атомів (наприклад групи СН₃), перекриваються з діапазонами для атомів іншого типу (нариклад, СН₂ і СН). Тому на підставі тільки величин хімічних зсувів далеко не завжди вдається ідентифікувати такі атоми вуглецю. Ситуація ускладнюється також тим, що, на відміну від протонних спектрів, вуглецеві спектри, виміряні за умов широкосмугового декаплінгу на протонах (саме такі спектри вимірюються найбільш часто), не містять інформації про спін-спінову взаємодію. В такому випадку мультиплетну структуру вуглецевих сигналів не можна долучити до інтерпретації спектру.

Якщо вуглеводневий радикал сполучений з функціональною групою, то хімічні зсуви його вуглецевих сигналів можуть значно змінюватися. Дія функціональної групи швидко зменшується в міру віддалення від неї, але може бути виявлена навіть на відстані в 5 хімічних зв’язків. Найчастіше під впли­вом гетероатомів сигнали ядер вуглецю зміщуються в слабке поле. Винят­ком є атоми важких галогенів (Вr, І). У сполуках, які містять такі атоми, сигнали ядер атомів вуглецю, що безпосередньо зв'язані з ними, зміщуються в сильне поле відносно незаміщених сполук, причому, коли таких атомів декілька, зміщення можуть дося­гати сотень мільйонних часток. В сильному полі знаходяться також сигнали атомів вуглецю, що зв’язані з металами в металорганічних сполуках, а також з кремнієм, бором або іншим атомом, електронегативність якого менша, ніж у вуглецю. Нарешті, слід відмітити так званий „g-ефект” – зсув сигналів ядер в сильне поле під впливом електроноакцепторних замісників, що знаходяться у g-положенні, тобто на відстані трьох хімічних зв’язків від ядра, що розглядається.

Атоми вуглецю, що сполучені кратними зв'язками, поглинають в істотно слабкішому полі, ніж у відповідних насичених сполуках. Так, в олефінових, ароматичних і гетероциклічних сполуках діапазон хімічних зсувів ¹³С становить 100—140 м. ч. Сигнали алкінів розташовані в більш сильному полі (70—90 м. ч.).

У найслабкішому полі поглинають атоми вуглецю, що зв'язані подвійним зв'язком з атомами кисню і, особливо, сірки. Так, сигнали ядер карбонільного атому вуглецю у кетонах розташовані в області 200—250 м. ч., а в аль­дегідах — 180—200 м. ч. У похідних карбонових кислот карбонільний атом вуглецю поглинає в дещо більш сильному полі — при 160—180 м. ч. Вуглець групи С =S поглинає в області 220—240 м. ч.

Уявлення про те, де саме поглинають атоми вуглецю у поширених молекулах,дають таблиці, що наведені нижче.

Таблиця 7. Положення у спектрі ¹³С сигналів метильних груп (м.ч.)

СН4 -2,1	СН3-СН3 5,9	Et-CH3 15,6	HC(CH3)2 24,3	CH3Cl 22,0
CH3Br 14,0	CH3J -21	CH3OH 49,3	CH3OCH3 59,4	CH3OPh 54,0
CH3OCOPh 51,3	CH3COPh 24,9	CH3COCH3 29	CH3Ph 21,0	CH3CN 0,5
N(CH3)3 47,5	CH3NO2 57,3	CH3SCH3 19,5	CH3SOCH3 43,5	(CH3)4C 31,5

Таблиця 8. Положення у спектрі ¹³С сигналів метиленових груп

(CH3)2CH2 16,1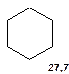

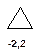
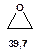
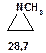
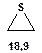
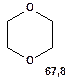
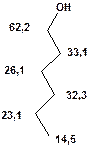
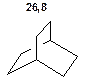
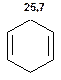
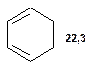
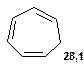
Таблиця 9. Положення у спектрі ¹³С сигналів метинових атомів

(СH3)3CH 25,2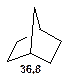

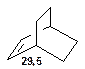
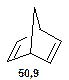
Таблиця 10. Положення в спектрі ¹³С сигналів карбонільної групи

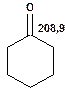
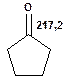
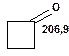
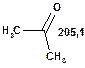
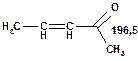
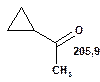
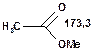
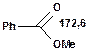
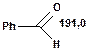
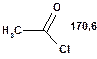
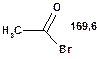
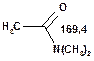
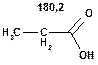
Таблиця 11. Положення в спектрі ¹³С сигналів олефінових атомів вуглецю

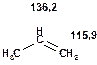
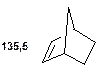
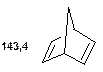
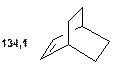
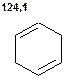
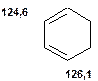
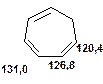
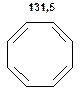
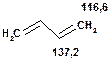
Таблиця 12. Положення в спектрі сигналів sp-гібридизованого атому вуглецю

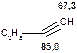
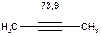
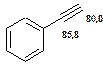
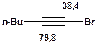
				СH3CN 117,8
HCN 109,1	CN- 168,8	Ph-CN 118,7	H2С=C=CHCH3 209

Таблиця 13Положення в спектрі сигналів ароматичних атомів вуглецю

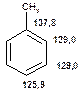
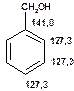
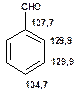
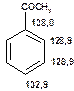
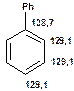
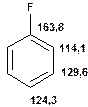
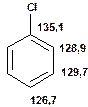
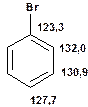
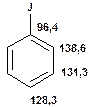
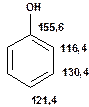
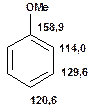
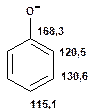
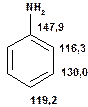
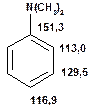
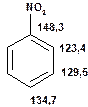
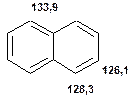
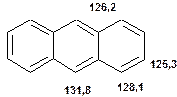
Таблиця 14. Положення в спектрі атомів вуглецю гетероциклічних фрагментів

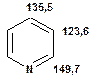
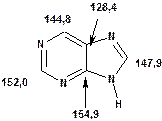
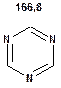
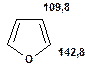
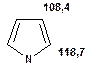
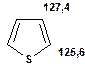
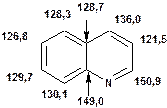
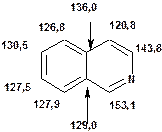
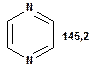
Таблиця 15. Положення в спектрі сигналів атомів вуглецю в заміщених поліциклічних гетероциклічних сполуках

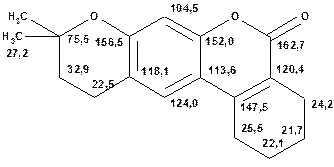
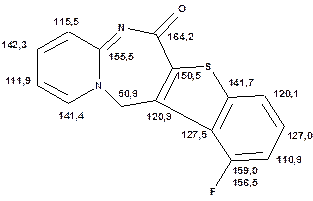
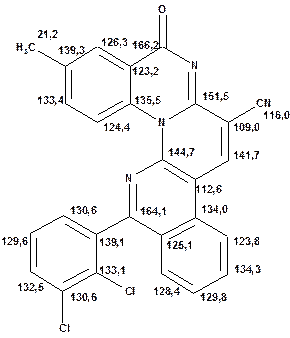
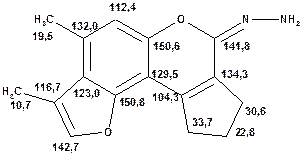
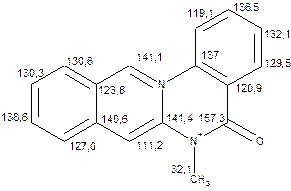
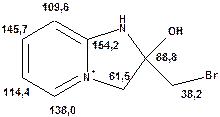
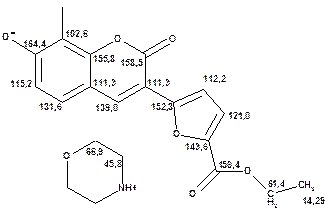
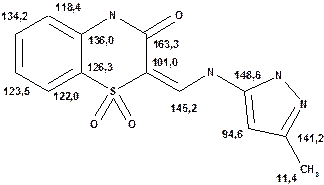
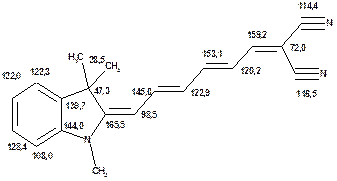
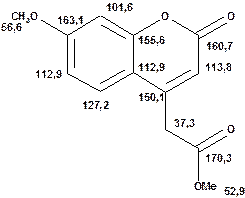
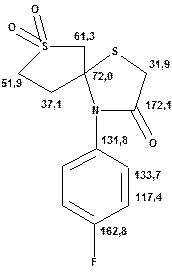
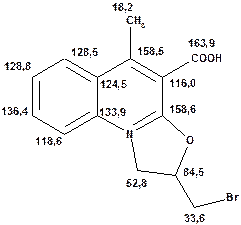
Речовини у таблицях підібрано таким чином, щоб вони містили більшість поширених структурних фрагментів органічних молекул. Тому за їхньої допомоги можна проводити інтерпретацію нескладних спектрів ЯМР на ядрах ¹³С. З цією метою треба мати перед очима вуглецевий спектр сполуки та її передбачувану структурну формулу. Досліджувану молекулу подумки потрібно розбити на структурні фрагменти, що є максимально близькими до тих, які вміщені в таблицях, та порівняти табличні величини хімічних зсувів зі зсувами сигналів у спектрі. Віднесення слід починати з тих структурних фрагментів, для яких похибка у віднесенні найменш ймовірна. Віднесення сигналів ядер вуглецю, що не містяться у таблицях, слід проводити в останню чергу, коли з’ясовано походження всіх інших сигналів. Воно повинне базуватися на тому, з якими гетероатомами сполучений атом вуглецю, сигнал якого бажано віднести, та на закономірностях впливу на хімічні зсуви сусідніх замісників.

За допомогою наведених таблиць можна передбачити, де поглинають атоми вуглецю певного типу. Але слід пам’ятати, що похибки передбачених таким чином хімічних зсувів можуть сягати +5м.ч. Тому у складних випадках надійно віднести вуглецеві сигнали вдається далеко не завжди. Це особливо чітко видно з наведених у Табл. 15 прикладів віднесення сигналів у складних гетероциклічних системах. Тут ми бачимо, що цілий ряд ядер ¹³С може поглинати у досить вузькому спектральному діапазоні, або навіть співпадати. Віднесення таких сигналів, що базується на табличних аналогіях, практично неможливе. Тому, якщо у Вашому спектрі міститься декілька сигналів, що за хімічними зсувами відрізняються лише на 2-5 м.ч., навіть не намагайтеся їх віднести без додаткових досліджень. Ваші віднесення не будуть достовірними. Ще однією проблемою для віднесення вуглецевих сигналів є великий вплив на них розподілення електронної густини в досліджуваній молекулі. Оскільки передбачити зміщення електронів заздалегідь не завжди можливо, певні сигнали у спектрі можуть спостерігатися у несподіваних, на перший погляд, ділянках спектру. Так, наприкінці таблиці 15 наведені віднесення сигналів для барвника, що має довгий поліметиновий ланцюг. Хімічні зсувивуглецевих атомів у цьому ланцюгу знаходяться в інтервалі від 120 до 150 м.ч., причому відмінність хімічних зсувів для сусідніх атомів, що з огляду на формулу, майже не відрізняються один від одного, можуть сягати 30 м.ч. Звісно, передбачити заздалегідь такі відмінності практично неможливо. Найбільш надійний підхід до віднесення вуглецевих сигналів полягає у вимірюванні спектрів гетероядерної кореляції ¹³С-¹Н через 1 зв’язок (HMQC, HSQC) та через 2-3 хімічних зв’язки (метод НМВС). За допомогою цих методів віднесення сигналів у вуглецевому спектрі можна здійснити цілком надійно. Єдиною умовою віднесення є наявність протонів у молекулі на відстані не більше трьох хімічних зв’язків від атомів вуглецю. Але, оскільки ця умова для більшості органічних молекул виконується, то сьогодні віднесення сигналів проводять саме такими методами.

3.4. Редагування спектрів на ядрах ¹³С

3.4.1. Редагування спектрів ¹³С за допомогою послідовності АРТ

Основною метою застосування широкосмугового декаплінгу на протонах при дослідженні гетероядер є підвищення інтенсивності сигналів, що відбувається при видаленні мультиплетної структури, і зменшення перекривань сигналів. Крім того, корисним є також підвищення інтенсивності сигналів за рахунок ЯЕО. Однак, недоліком широкосмугового декаплінгу є втрата інформації про спіновий зв'язок ядер Х з протонами. Внаслідок цього, в спектрах з широкосмуговим декаплінгом відсутня можливість розрізнити сигнали, наприклад, метильної і метиленової груп. Тому досить корисною була б методика запису повністю розв'язаного від протонів спектру, але зі збереженням інформації про мультиплетність сигналів. Для цього розроблено декілька багатоімпульсних послідовностей редагування спектрів, у яких мультиплетність можна визначити за знаком сигналів. Зараз вони широко застосовуються в дослідницькій практиці.

Один з методів редагування базується на тому, що після подачі первинного 90^о імпульсу поведінка утвореної ядрами ¹³С намагніченості залежить від того, зі скількома протонами зв’язаний той чи інший атом вуглецю. Тому, якщо після першого ¹³С імпульсу подати другий імпульс через інтервал часу D, то інтенсивність сигналів залежатиме від того, чи є атом первинним, вторинним, або третинним. Можна підібрати інтервал D так, що сигнали метильних груп будуть позитивними, а метиленових – негативними, або навпаки.

Прикладом відредагованого таким чином вуглецевого спектру є спектр камфори, 7, що зображений на Рис. 23б.

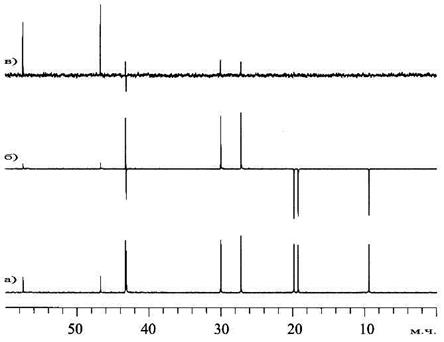
Рис. 23. Вуглецеві спектри камфори 7. (a) Звичайний вуглецевий спектр знятий в умовах широкосмугового декаплінгу (сигнал карбонільної групи не показаний), і відредаговані спектри; (б) параметри імпульсної послідовності підібрано так, щоб сигнали метильних та метиленових груп мали протилежну орієнтацію (знак); (в) послідовність налаштована так, що чітко проявляються лише четвертинні атоми вуглецю.

Найчастіше відредаговані спектри зображають таким чином, що сигнали груп СН є позитивними, а сигнали метиленових груп – негативними. Таким чином, мультиплетність вуглецевих сигналів виявляється закодованою в знаку сигналу. При цьому повертається частина інформації, що губиться при декаплінгу. У спектрах, які записані за допомогою даної послідовності, зберігається підвищення інтенсивності сигналів внаслідок ЯЕО. Якщо вибрати D=1/2J с., то інтенсивність сигналів всіх атомів вуглецю, що зв’язані з атомами водню, буде дорівнювати нулю і у спектрі залишаться тільки сигнали четвертинних (не зв’язаних з Н) атомів вуглецю (Рис. 23в). Точність редагування істотно залежить від правильності вибору інтервалу D, який визначається величиною J. Інтервал D можна назвати „керуючим інтервалом”, оскільки від нього залежать результати редагування. Керуючий інтервал застосовується і в інших багатоімпульсних послідовностях.

Оскільки в реальних молекулах КССВ перебувають у певному, досить великому діапазоні, доводиться вибирати деяке компромісне значення D. Протон-вуглецеві КССВ через один зв'язок лежать у діапазоні від 125 до 250 Гц, причому найчастіше зустрічаються їхні величини від 130 до 170 Гц. Тому для молекул, що містять ароматичні фрагменти і електронегативні групи в аліфатичному ланцюгу, типова величина D = 7 мілісекунд (¹J_CН = 140 Гц). Якщо реальні КССВ перебувають далеко від цього діапазону, то відповідні сигнали можуть мати несподіваний знак і інтенсивність. Так буває при вивченні похідних ацетилену, для яких характерні значно більші КССВ. Тому для отримання оптимальних результатів цим методом іноді доводиться дещо змінювати інтервал D.

3.4.2. Редагування спектрів за допомогою послідовності DEPT

Методика редагування вуглецевих спектрів, що була описана вище, не завжди дає задовільні результати. В ряді випадків відредаговані спектри містять сигнали із значним викривленням фази. В простих спек