Детерминированный акцептор

Детерминированныйакцептор 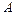с конечным числом состояний (конечный акцептор, анализатор) задается пятеркой:

, где

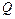- конечное множество состояний;

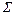- конечное множество допустимых входных символов;

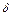- отображение множества в множество :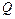

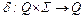. Для детерминированного акцептора это отображение является функциональным, и называется функцией переходов;

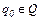- начальное состояние акцептора;

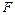- множество состояний, называемых заключительными или принимающими состояниями акцептора: .

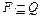Пара 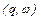называется конфигурацией автомата 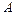, если 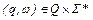(т.е. если 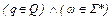). В процессе работы акцептора цепочка 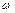представляет собой последовательность символов на входной ленте, начинающуюся с символа, обозреваемого головкой в состоянии 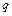, и всеми символами еще не считанными с ленты, т.е. находящимися справа от обозреваемого символа.

Конфигурация 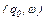называется начальной. При этом 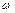- это цепочка символов, которая должна быть проанализирована акцептором 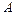и либо принята им (классифицирована как принадлежащая языку , задаваемому акцептором), либо отвергнута как не принадлежащая языку .

Пара 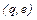, где 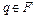называется заключительной или допускающей. 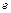означает, что вся входная цепочка считана с ленты.

Такт автомата 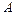представляется бинарным отношением ⊢ 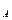(или ⊢, если 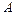подразумевается), определенным на конфигурациях.

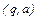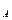
Отношение ⊢ 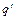означает следующее:

- автомат 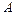находится в состоянии 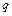и его входная головка обозревает ячейку ленты с символом ;

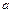- в результате выполнения данного такта автомат перейдет в состояние 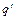и сдвинет входную головку на одну ячейку вправо.

Необходимо отметить, что существуют грамматические модели, не входящие в иерархию Хомского. Такие грамматики были разработаны в процессе поиска порождающих механизмов, которые бы лучше представляли весь синтаксис и/или семантику языков программирования.