Классификация языков по Хомскому; порождающие грамматики.
Классификация грамматик по Хомскому основывается на ограничениях, накладываемых на продукции 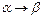 , т.е. ограничения на виды цепочек, обозначенных как
, т.е. ограничения на виды цепочек, обозначенных как 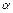 и
и  .
.
В приводимой в табл.3.1 классификации грамматик по Хомскому разные грамматики отнесены к одному типу на том основании, что они порождают один класс языков. Так, например, грамматики типа 3, называемые праволинейными, регулярными, автоматными – это разные грамматики, но порождаю один класс языков. Один класс в том смысле, что любой язык, порождаемый одной из перечисленных грамматик, может быть порожден и любой другой.
Таблица 3.1
| Названия грамматики | Ограничения на правила (на продукции) |
| Тип 0 (или общего вида, или без ограничений) | Нет никаких ограничений на 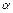 и и  . .
|
| Тип 1 (контекстно-зависимая (КЗ); неукорачивающая; непосредственных составляющих (НС) ) | Ограничения только на длины цепочек 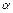 и и  , а именно: , а именно:  . Поэтому в грамматике нет правил вида . Поэтому в грамматике нет правил вида 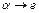 . .
|
| Тип 2 (контекстно-свободная (КС); безконтекстная) | Каждая продукция имеет вид: 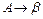 , , 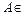 Ɲ, Ɲ, 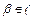 Ɲ Ɲ 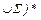 , т.е. цепочка , т.е. цепочка 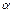 состоит строго из одного нетерминала ( состоит строго из одного нетерминала (  ). Причем, возможны продукции ). Причем, возможны продукции 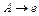
|
| Тип 3 (праволинейная или правостороняя; леволинейная или левосторонняя; регулярная; автоматная ) | Каждая продукция имеет вид: 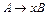 или или 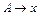 , где , где 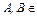 Ɲ , Ɲ , 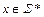 т.е. т.е. 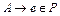 , , 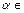 Ɲ, Ɲ,  или или 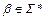 Ɲ (конкатенация цепочек из Ɲ (конкатенация цепочек из  с нетерминалом из Ɲ) с нетерминалом из Ɲ)
|
В правосторонней (праволинейной) грамматике цепочки удлиняются только вправо, а продукции имеют вид 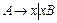 , где
, где 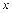 - цепочка терминалов. В левосторонней (леволинейной) грамматике цепочки удлиняются только влево, а продукции имеют вид
- цепочка терминалов. В левосторонней (леволинейной) грамматике цепочки удлиняются только влево, а продукции имеют вид 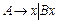 , где
, где 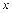 - цепочка терминалов. Автоматная грамматика представляет собой частный случай правосторонней или левосторонней грамматики, в которой цепочка терминалов упростилась до одного символа. Таким образом, в автоматной грамматике продукции имеют вид
- цепочка терминалов. Автоматная грамматика представляет собой частный случай правосторонней или левосторонней грамматики, в которой цепочка терминалов упростилась до одного символа. Таким образом, в автоматной грамматике продукции имеют вид 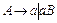 или
или  , где
, где 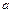 - это цепочка из одного символа. Причем, если
- это цепочка из одного символа. Причем, если  , то
, то 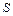 не встречается в правых частях правил. Для любой праволинейной грамматики
не встречается в правых частях правил. Для любой праволинейной грамматики 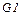 можно построить эквивалентную ей автоматную
можно построить эквивалентную ей автоматную 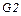 . Эквивалентную в том смысле, что языки, порождаемые грамматиками
. Эквивалентную в том смысле, что языки, порождаемые грамматиками 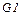 и
и 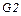 , будут совпадать.
, будут совпадать.
Продукция, т.е. правило, вида 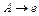 обычно называется
обычно называется 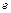 - продукциейили
- продукциейили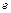 - правилом.
- правилом.
Подчеркнем, что КС грамматика, содержащая 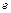 - правила, не является грамматикой НС.
- правила, не является грамматикой НС.
Из сравнения грамматик видно, что
n грамматика типа 3 является частным случаем грамматики типа 2;
n грамматика типа 2 является частным случаем грамматики типа 1, если не содержит 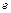 - продукций;
- продукций;
n грамматика типа 1 – частный случай грамматики типа 0.
Будем считать, что если язык 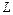 порождается грамматикойтипа
порождается грамматикойтипа 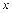 , то
, то 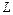 называется языкомтипа
называется языкомтипа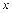 .
.
Следует отметить, что если язык задан какой-то грамматикой, то это еще не значит, что его нельзя породить менее мощной грамматикой. Например, КС-грамматика с продукциями 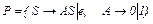 порождает язык {0,1}*. Этот же язык можно породить менее мощной грамматикой: праволинейной с продукциями
порождает язык {0,1}*. Этот же язык можно породить менее мощной грамматикой: праволинейной с продукциями 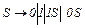 или леволинейной с продукциями
или леволинейной с продукциями 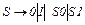 .
.
Дата добавления: 2015-08-11; просмотров: 1069;
