Скорость витания твердой частицы в потоке воздуха

Рассмотрим свободное падение твердых частицы в воздухе. Пусть твердая частица, имеющая массу m (рис.46) свободно без толчка падает из т. О, которую принимаем за начало координат. Ось У по которой осуществляется падение частицы направим вертикально вниз. Под действием силы тяжести равной P=m∙g частица будет падать, оставаясь, все время на оси У.

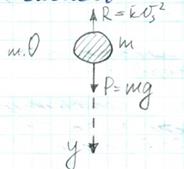Рис.46

В первый начальный момент времени частица будет падать под действием ускорения свободного падения (g=9,81м/с²), но т.к. воздух оказывает сопротивление движению частицы через некоторое время частица будет падать с определенной постоянной скоростью без ускорения. Т.о. скорость падения частицы в вязкой среде, которой является воздух не может беспредельно возрастать, а с течением некоторого времени достигает своего наибольшего значения υ_S, которая сохраняет во все последующее время падения. Если твердую частицу поместить в восходящий воздушный поток, частица зависнет в нем, т.е. будет витать.

Средняя скорость восходящего воздушного потока, при которой частица ни будет иметь вертикального перемещения, а будет находится во взвешенном состоянии называется скоростью витания.

Скорость витания частицы равна постоянной скорости падения частицы в неподвижном воздухе.

Таким образом, на твердую частицу действуют две силы:

1) сила тяжести; 2) сила сопротивления воздуха R. R может быть записана как:

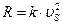, (79)

где υ_S – скорость восходящего потока воздуха

к – коэффициент пропорциональности.

При достижении падающей частицей постоянной скорости сила тяжести равна силе сопротивления Р=R, тогда:

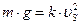(80)

Тогда:

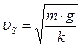(81)

Сопротивление среды движущемуся в ней воздуху можно записать в следующем виде:

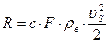(82)

где с – коэффициент пропорциональности, с=ƒ(Re)

F – площадь проекции тела на плоскость перпендикулярную вектору скорости, м²

ρ_в – плотность среды (воздуха).

Следовательно, из выражений (79) и (82) заключаем, что коэффициент пропорциональности к может быть записан в виде:

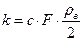(83)

А скорость падения частицы в воздухе с учетом выражения (83) будет:

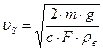(84)

Коэффициент пропорциональности с в выражении (84)может быть определен по формуле Клячко:

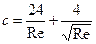(85)

С достаточной для практике точностью (85) можно записать:

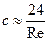(85а)

Подставляя выражение (85а) в функцию (84) при развернутом виде Re:

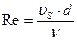
ν – коэффициент кинематической вязкости воздуха, м²/с

Численное значение скорости υ_S можем определить:

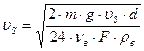(86)

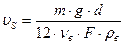(87)

Для частицы, имеющей форму близкую к шару, масса частицы:

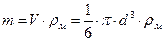(88)

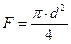
Следовательно, выражение (88) можно записать в виде:

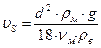(89)

где ρ_м – плотность материала частицы.

Формула (89) справедлива для частиц, имеющих форму шара с размером до 100 мк. Такая пыль, например, выделяется при обработке древесины на шлифовальных станках. Все же другие отходы и материалы, которые могут транспортироваться системами пневмотранспорта, имеют большие размеры и по форме отличаются от формы шара. Поэтому скорость витания этих частиц в инженерной практике определяется по эмпирическим формулам, которые справедливы для частиц определенной формы данного материала. Процесс пневматического транспортирования частиц в вертикальных воздуховодах возможет, только если скорость воздушного потока превышает максимальное значение скоростей витания частиц.