Однородная плоская стенка

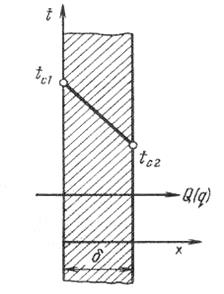
Рис. 2.2. Стационарное распределение температуры по толщине однородной плоской стенки

Про­стейшей и очень распространенной задачей, решаемой теорией теплообмена, является определение плотности тепло­вого потока, передаваемого через плоскую стенку толщиной δ, на повер­хностях которой поддерживаются темпе­ратуры t_С1 и t_С2 (рис. 2.2). Температура изменяется только по толщине пласти­ны — по одной координате х. Такие за­дачи называются одномерными, решения их наиболее просты, и в данном курсе мы ограничимся рассмотрением только одномерных задач. В стационарных условиях, когда энергия не расходуется на нагрев, плот­ность теплового потока неизменна по толщине стенки. В большинстве практи­ческих задач приближенно пред­полагается, что коэффициент тепло­проводности λ не зависит от температуры и одинаков по всей толщине стенки.

Зна­чение λ находят в справочниках при температуре

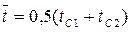
средней между температурами поверхно­стей стенки. Зависимость для расчета плот­ности теплового потока:

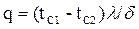
или

.

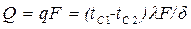Отношение λF/δ называется тепло­вой проводимостью стенки, а обратная величина δ/(λF) термическим сопротив­лением стенки и обозначается R_λ. Пользуясь понятием термического сопро­тивления, формулу для расчета теплово­го потока можно представить в виде

.

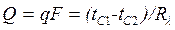2.5.2.Многослойная плоская стенка

Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоев:

.

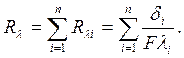
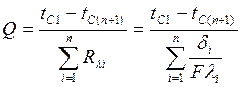Обобщен­ная формула для расчета температуры t_C за любым слоем:

.

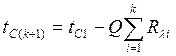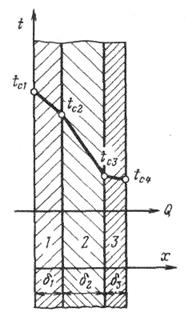
Рис. 2.3. Стационарное распределение температуры по толщине многослойной плоской стенки