Гиперболический параболоид.

Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в неко-торой специально выбранной прямоугольной системе

координат, имеет вид: 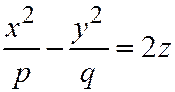, (3)

где 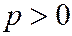, 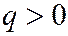. Для гиперболического параболоида (3) плоскост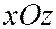и и 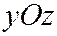являются плоскостями симметрии, а ось 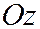осью симметрии.

Ось симметрии для гиперболического параболоида называется просто его осью. Точка в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид имеет вершину в начале координат.

Плоскост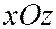и и 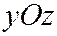, являющиеся для гиперболического параболоида плоскостями симметрии, называются главными плоскостями гиперболического параболоида.

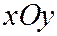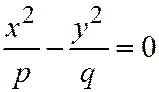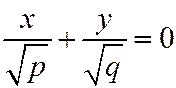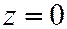Плоскость пересекает гиперболический пара-болоид (3) по прямым: ; или ,

; и , .

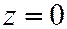Плоскость 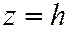, параллельная плоскости 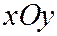, пересекает гиперболический параболоид по гиперболе 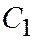: 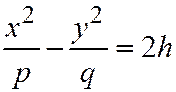, 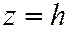. (4)

Если 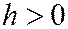, то эти уравнения можно параписать в виде: 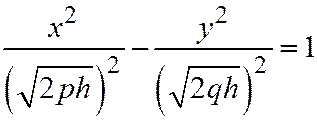, 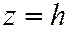. Это гипербола, расположенная в плоскости 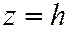с центром в точке 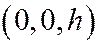, действительная ось которой параллельна оси 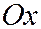, а мнимая - параллельна оси .

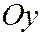Если 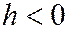, то уравнения линии сечения можно представить в виде: 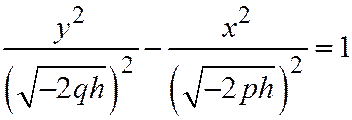, 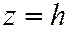. Это гипербола, расположенная в плоскости 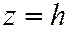с центром в точке 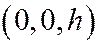, действительная ось которой параллельна оси 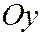, а мнимая - параллельна оси .

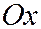Асимптоты всех гипербол, получающихся при пересечении гиперболического параболоида (3) плос-костями 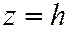, 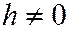параллельны прямым, по которым этот параболоид пересекается с плоскостью .

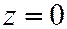Плоскость 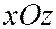пересекает гиперболический параболоид (3) по параболе 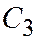: 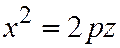, , 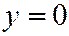а плоскость 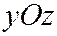по параболе : , .

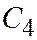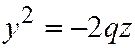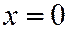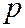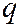Мы видим, что числа и являются параметрами парабол, получающихся в сечении гиперболического параболоида (3) его главными плоскостями.

Рассмотрим сечения гиперболического параболоида (3) плоскостями, параллельными плоскостям 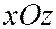, т.е. плоскостями, выражаемыми уравнением .

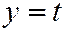Уравнение линии сечения будет следующим:

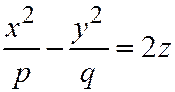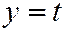, , или 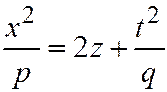, , 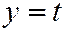или:

, .

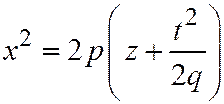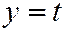Эти уравнения выражают параболу 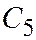с вершиной в точке 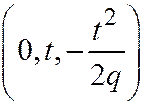, ось которой выражается уравнением: 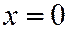, 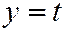а направление совпадает с положительным направлением оси 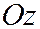. Параметр параболы 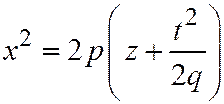, 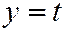равен 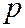, т.е. параметру главного сечения гиперболического параболоида плоскостью .

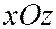Аналогичная картина получается и для сечений гиперболического параболоида (3) плоскостями, параллельными плоскости 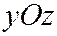(См. рисю209)

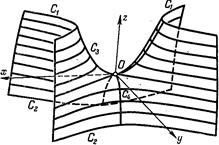
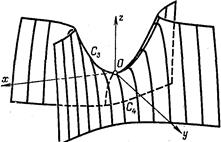
Рис. 209. Рис. 210.

Таким образом, гиперболический параболоид может быть образован параллельным переносом параболы 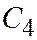при котором вершина параболы 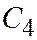перемещается по параболе 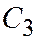. Плоскость параболы 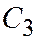перпендикулярна плоскости параболы 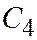, а оси этих парабол параллельны и противоположно направлены (См. рис. 208).