Парадоксы формулы Журавского
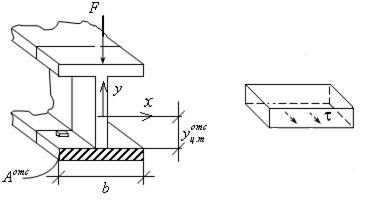
рис.15.18. рис.15.19.
Рассмотрим малый элемент, высота которого много меньше толщины полки (см. рис. 15.18.). По формуле Журавского.
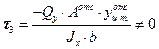(15.24)
С другой стороны, согласно рис.15.19 на верхней грани никаких воздействий нет, поскольку это свободная поверхность полки. Из условия равновесия по оси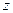 
(рис. 15.19) получим, что 
.
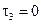Это противоречие вызвано тем, что в сопромате много пренебрежений малыми величинами. Если построить эпюру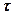 
по высоте двутавра по формуле Журавского, то получим картину, изображенную на рис.15.20. В данной задаче в полке значения напряжения 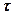(вычисленные по формуле (15.24)) хоть и отличны от 0, но очень малы (обычно они составляют менее 5% от 
).
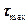Ясно, что в расчетах на прочность малые напряжения 
не используются, а их уточнение бессмысленно.
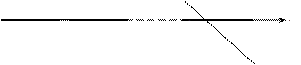
рис.15.20.
(Отмеченное выше противоречие аналогично противоречию вида 2.48 ≈ 2.5, из которого тоже вытекает, что якобы 0.02=0).
15.10. О максимальных касательных напряжениях(τzy )max
В большинстве случаев (τzy )max достигает наибольшего значения на уровне центра тяжести сечения. Это относится к сечениям прямоугольной, круглой, двутавровой формы и им подобным. Однако в нестандартных случаях необходимо строить эпюру касательных напряжений, т.к. максимальные касательные напряжения действуют на сечение не всегда на уровне центра тяжести. Например,нетрадиционное распределение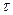 
по высоте сечения получается для балки с сечением вида креста. В области центра тяжести ширина сечения много больше, чем у вертикальных стенок. Значит, в формуле Журавского в знаменателе величина b будет большая, следовательно, и напряжения в полке (горизонтальной части сечения) будут малы. Тогда эпюра 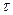будет иметь вид, приведенный на рис. 15.21.
рис. 15.21
Таким образом,(τzy )max возникает не всегда на уровне центра тяжести сечений.
Дата добавления: 2015-08-11; просмотров: 1076;