Смертность.

Численность некоторой группы особей, родившихся в одно и то же время, в течение жизни непрерывно снижается в результате отмирания части особей. Смертность организмов проявляется даже в тех случаях, когда условия жизни вполне благоприятны. В этих случаях говорят о минимальной смертности, природа которой связана с дефектами физиологического развития, приводящими к гибели отдельных организмов. В иных случаях смертность может сильно меняться в зависимости от условий внешней среды (например, условий питания, загрязненности, вследствие действия неблагоприятных абиотических факторов).

Смертность, как и рождаемость, выражается числом особей, погибших за данный период времени,но чаще в виде относительной или удельной величины. Такой величиной может быть процент особей, погибших в единичный отрезок времени, или их доля от начальной численности группы. У большинства организмов интенсивность смертности меняется в течение жизни. Как правило, она высока на ранних стадиях развития, затем снижается и вновь возрастает к старости.

Известно, что каждый организм характеризуется своей индивидуальной продолжительностью жизни, которая может изменяться в некоторых присущих данному виду пределах. Если говорить о средней продолжительности жизни группы организмов, например средней продолжительности жизни группы рыб, появившихся на свет в одном и том же году, то эта продолжительность будет определяться величи­ной смертности. Чем больше смертность, тем меньше средняя продолжительность жизни группы, и наоборот.

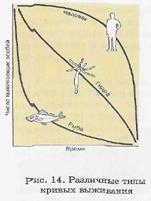
Представленные на рисунке 1 кривые называют кривыми выживания. Кривые выживания - графическая зависимость числа выживших особей от их возраста при условии, что первоначальное число особей составляет 100 или 1000.Обычно при построении этих кривых по оси абсцисс откладывают время или возраст, а по оси ординат – число выживших особей.

Различают пять основных типов кривых выживания.

1. Кривая I - характерна для популяций, в которых большинство особей имеет продолжительность жизни, близкую к максимально возможной для данного вида, и умирают в течение короткого отрезка времени. Эту форму кривой называют выпуклой. Она свойственна насекомым, многим крупным млекопитающим, человеку.

2. Кривая II - теоретическая, отражает равную вероятность гибели особей в любом возрасте, то есть коэффициент смертности остается постоянным в течение всей жизни особей. Например, у многих природных популяций птиц и насекомых, постоянно находящихся в оптимальных условиях.

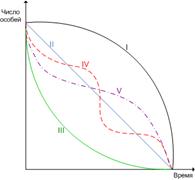
3. Кривая III соответствует очень высокой смертности в раннем возрасте, а для особей, переживших этот период, вероятность смерти низка. Эта форма кривой - вогнутая. К таким популяциям относятся многие растения, беспозвоночные и рыбы.

4. Кривая IV имеет ступенчатый характер и показывает, что при переходе от одной стадии развития к другой происходит резкое изменение выживания особей.

5. Кривая V - имеет S-образную форму, приближающуюся к теоретической кривой.

Сильно выпуклая кривая (1) характерна для видов, у которых смертность резко повышается лишь к концу жизни, а до этого она остается низкой. Такой тип кривой характерен для многих видов крупных животных и, конечно, для человека.

Другой крайний вариант – сильно вогнутая кривая (3). Она получается, если смертность очень высока на ранних стадиях жизни. Хорошей иллюстрацией этого типа служат рыбы, устрицы или другие двустворчатые моллюски, а также дубы. Но как только особи подрастают и хорошо приживаются на подходящем субстрате, их смертность резко снижается.

К промежуточному типу относятся кривые выживания таких видов, у которых смертность мало изменяется с возрастом и остается более или менее одинаковой в течение всей жизни данной группы.

Форма кривой выживания очень часто изменяется при изменениях плотности популяции. При возрастании плотности она становится более вогнутой, иными словами, при уве­личении численности организмов их смертность возрастает.