Физические характеристики вибрации

По ГОСТ 24346 – 80 под вибрацией понимается движение точки или механической системы, при котором происходит поочередное возрастание и убывание во времени значений любой величины, её характеризующей.

По механизму генерации различают вибрации с силовым, кинематическим и параметрическим возбуждением.

Силовое возбуждение вибрации – это возбуждение вибрации системы вынуждающими силами и моментами. Источниками их являются: возвратно-поступательные движущиеся системы (кривошипно-шатунные механизмы, ручные вибраторы и перфораторы, вибротрамбовки, виброплиты, вибробункеры и т.п.); неуравновешанные вращающиеся массы (ротора насосов и ГТД, ручные электрические и пневматические шлифовальные машины, режущий инструмент станков, вентиляторы и т.п.); ударные системы (ковочные и штамповочные молоты, подшипниковые узлы, зубчатые передачи и т.п.).

Кинематическое возбуждение вибрации – возбуждение вибрации системы сообщением каким-либо ее точкам заданных движений, не зависящих от состояния системы. Причинами его являются воздействие профиля дороги на автомобили и строительно-дорожные машины, электрокары и ручные тележки в помещениях, колебания пола помещений и т.п.

Параметрическое возбуждение вибрации – возбуждение колебаний и вибрации системы не зависящим от состояния системы изменением во времени одного или нескольких ее параметров (массы, момента инерции, коэффициентов жесткости и сопротивления). Источниками являются двигатели внутреннего сгорания при изменении давления газов в цилиндрах, пневматические двигатели и т.п.

По характеру изменения во времени различают колебания детерминированные (периодические или почти периодические), случайные (стационарные или нестационарные) и импульсные или затухающие, которые могут быть простыми и сложными.

Сложные колебательные процессы могут быть представлены в виде простых гармонических синусоидальных колебаний с помощью ряда Фурье.

Колебания подразделяются на свободные и вынужденные. Свободные колебания – вибрации системы, происходящие без переменного внешнего воздействия и поступления энергии извне. Вынужденные колебания – вибрации системы, вызванные и поддерживаемые силовым или кинематическим возбуждением.

Основными понятиями теории колебаний для вибрации являются:

1) вибрационные параметры: виброперемещение, виброскорость и виброускорение;

2) механический импеданс;

3) собственная частота.

Основными величинами, характеризующими вибрацию, происходящую по синусоидальному закону, являются:

· амплитуда виброперемещения S_а– величина наибольшего отклонения колеблющейся точки от положения равновесия;

· амплитуда виброскорости V_а – максимальное значение скорости колеблющейся точки;

· амплитуда виброускорения а_а – максимальное значение ускорения колеблющейся точки;

· период колебаний Т– наименьший интервал времени, через который при периодических колебаниях повторяется каждое значение колеблющейся величины, характеризующей вибрацию;

· частота колебаний f– величина, обратная периоду колебаний.

Виброскорость и виброускорение связаны с виброперемещением и частотой ко­лебаний соотношениями:

V = 2 p × f × S и a = (2 p × f)² × S

Учитывая, что абсолютные значения величин, характеризующих вибрацию, изменяются в очень широких пределах, в практике виброакустических исследований и инженерных расчетах используют логарифмические уровни колебаний. Под ним понимается сравнительная характеристика колебаний двух одноименных физических величин, пропорциональная десятичному логарифму отношения оцениваемого и исходного значений величины

L = 20 × lq (b × b_о^–1),

где b – оцениваемое значение величины (скорость, ускорение и т.п.);

b_о – исходное значение величины (скорости, ускорения и т.п.).

Так, например, уровни виброскорости и виброускорения определяются соответственно как

L_V = 20 × lq (V × V_o^–1) и L_A = 20 × lq (a × a_o^–1),

где V и а – оцениваемые значения соответственно виброскорости и виброуско­рения;

V_o и а_о – исходные (пороговые) значения виброскорости и виброускорения.

Согласно международному соглашению принято:

V_о = 5 × 10 ^{– 8} м/с и а_о = 3 × 10 ^{– 4} м/с².

Уровни колебаний (вибрации) измеряются в децибелах (дБ).

В общем случае физическая величина, характеризующая вибрацию (например, виброскорость) является некоторой функцией времени: V = V(t). Математическая теория показывает, что такой процесс можно представить в виде суммы бесконечно долго длящихся гармонических (синусоидальных) колебаний с различными амплитудами и периодами. В случае периодических колебаний частоты этих составляющих кратны основной частоте колебаний (процесса):

f_n = n × f₁,

где n = 1,2,3,..;

f₁ – основная частота колебаний.

Основной характеристикой в производственной безопасности или охране труда является спектр вибрации, под которым понимается совокупность соответствующих гармоническим составляющим значений величины, характеризующей колебания (вибрации), в которой указанные значения располагаются в порядке возрастания частот гармонических составляющих. Периодическим и почти периодическим колебаниям соответствует дискретный спектр, непериодическим – непрерывный спектр. Если колебания представляют собой наложение периодических и случайных колебаний, то спектр имеет смешанный характер.

Интенсивность вибрационных воздействий на человека, приборы и другие объекты зависит от частоты. Поэтому весь диапазон частот колебаний принято разбивать на отрезки (полосы частот) и определять уровни вибрации для каждой полосы в отдельности. В качестве стандартных частотных полос при оценке вибрационной безопасности принимают октавные полосы, у которых отношение верхних граничных частот к нижним частотам равно 2. Каждую октавную полосу принято обозначать среднегеометрическим значением ее граничных частот, определяемым по формулам

f_c = (f_max × f_min) ^0,5 = 2 ^0,5 f_min @ 1,41 f_min ,

где f_min – нижняя, а f_max – верхняя граничная частота, Гц, причем f_max = 2 f_min.

При необходимости октавные полосы делят на третьоктавные, для которых f_max = 2^1/3f_min @1,26 f_min. Например, первая октавная полоса имеет граничные частоты 0,7 и 1,4 Гц, а ее среднегеометрическая частота f_c = 1 Гц; следующая, соответственно 1,4….2,8 Гц и 2 Гц и т. д.

Механический импеданс (Z) определяется как отношение вынуждающей силы (F), приложенной к системе, к результирующей колебательной скорости υ в точке приложения силы

.

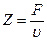Собственная частота — это частота свободных колебаний системы, т.е. колебаний без переменного внешнего воздействия и поступления энергии.

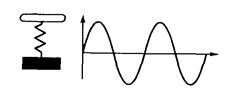
Рис. 11.1. Собственная часто­та колебаний

Собственная частота колебаний системы (f₀), представленной на рис. 11.1, определяется по формуле:

,

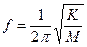где К — жесткость пружины; М — масса груза.

При равенстве собственной частоты колебаний системы частоте вынужденных колебаний возникает явление резонанса, приводящее к резкому увеличению амплитуды колебаний.