Распределение концентрации неравновесных носителей заряда

Вследствие инжекции электронов в дырочный полупроводник возрастает их концентрация в приповерхностной области, что ведет к возникновению диффузии вдоль оси x. Диффундируя вглубь полупроводника электроны, встречаясь с дырками, рекомбинируют. Так как процесс рекомбинации носит вероятностный характер, то различные электроны, прежде чем рекомбинировать, успевают проникнуть вглубь полупроводника на различные расстояния. Вследствие этого, концентрация электронов оказывается распределенной неравномерно. Количество электронов, пересекающих в единицу времени единичную площадку, перпендикулярную направлению диффузии, пропорционально градиенту концентрации электронов, то есть:

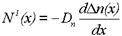. (1.26)

При инжекции дырок в электронный полупроводник количество дырок, диффундирующих через сечение x, определяется аналогичным образом, то есть:

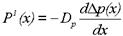, (1.27)

где D_n и D_p - коэффициенты диффузии электронов и дырок.

Поскольку электроны и дырки диффундируют в направлении убывания их концентрации, то это обстоятельство учитывается знаком минуса.

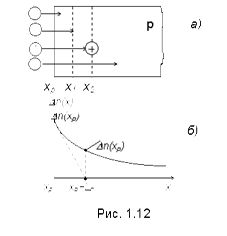
Для нахождения закона распределения избыточной концентрации вдоль оси x выделим внутри полупроводника объем, ограниченный сечениями x₁ и x₂ , приняв площадь поперечного сечения равной 1 см² (рис. 1.12). Через сечение x₁ в соответствии с (1.26) за время dt проходит D n(x₁,t) электронов:

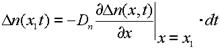, (1.28)

а через сечение x₂ проходят D n (x₂,t) электронов:

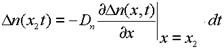. (1.29)

При этом часть электронов встречается с дырками и рекомбинирует. Количество рекомбинирующих электронов определяется временем жизниt _n, интервалом времени dt и объемом dx:
.

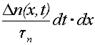Таким образом, изменение количества электронов в объеме dx за время dt можно представить в виде:

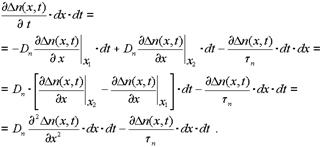(1.30)

Последнее уравнение можно записать в виде:

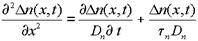. (1.31)

Избыточные носители заряда, диффундируя в объеме полупроводника, за время своей жизни t _n перемещаются в среднем на расстояние .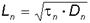

Следовательно:

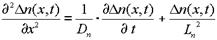. (1.32)

Полученное уравнение называют уравнением непрерывности для электронов. Оно учитывает диффузионное движение носителей заряда и их рекомбинацию. Интегрируя это уравнение при известных начальных и граничных условиях можно определить D n(x,t).

В случае непрерывной инжекции, поддерживающей в сечении x_p постоянное значение избыточной концентрации n(x_p) процессы не будут зависеть от времени. Тогда уравнение (1.32) можно записать в виде:

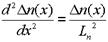. (1.33)

Решение этого уравнения имеет вид:

.

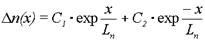Определим граничные условия: при x=x_p получаем D n (x)=D n (x_p), при x=Ґполучаем D n (x)=0. Величина Dn (x_p) обычно известна. Следовательно,

C₁=0, а

.

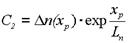Таким образом, распределение избыточной концентрации вдоль оси x характеризуется уравнением:

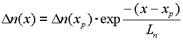, (1.34)

из которого следует, что диффузионная длина L_n представляет собой расстояние, на котором избыточная концентрация уменьшается в ераз. (Рис. 1.12,б).

В полупроводниковых приборах часто встречаются такие случаи, когда инжекция осуществляется в тонкую область толщиной w< L_n . В этом случае решение уравнения (1.34) имеет вид:

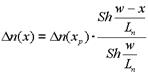. (1.35)

При условии w<<L_n тригонометрические функции можно заменить их аргументами, тогда:

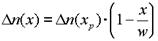, (1.36)

то есть распределение избыточных носителей становится линейным.

Распределение избыточной концентрации дырок вдоль оси x имеет такой же характер, как и распределение концентрации электронов, но при этом диффузии дырок не возникает, так как при смещении дырок в направлении оси x отрицательный заряд инжектированных электронов оказывается не скомпенсированным положительным зарядом неравновесных дырок, вследствие чего возникает внутреннее электрическое поле, препятствующее диффузии дырок. Формально можно считать, что диффузионное движение дырок происходит, но одновременно с этим происходит встречное движение дырок, обусловленное возникшим внутренним полем. Эти встречные потоки дырок уравновешивают друг друга, поэтому реального движения дырок не происходит.
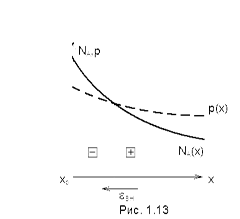
Аналогичное явление имеет место в полупроводниках с неравномерным распределением примесей. На рис. 1.13 представлен случай, когда концентрация акцепторной примеси N_A(x) убывает в направлении оси x. Полагаем приблизительно, что все акцепторы ионизированы и, пренебрегая наличием в полупроводнике электронов, можно считать, что p(x)» N_A(x), то есть закон распределения концентрации дырок такой же, как закон распределения акцепторов. В этих условиях неравномерное распределение концентрации дырок вдоль оси xдолжно вызвать диффузию дырок, в результате чего снизится их концентрация у поверхности и возрастет их концентрация в глубине полупроводника, следовательно, отрицательные заряды акцепторов окажутся не скомпенсированными и возникнет внутреннее электрическое поле, препятствующее диффузии дырок. Если в такой полупроводник через сечение x_p инжектировать электроны, то внутреннее поле для этих электронов окажется ускоряющим. В этом случае перемещение электронов в дырочные области будет происходить как за счет диффузии, так и под действием сил внутреннего поля.