Движущий и полезный напоры контура циркуляции.
Испарительные поверхности барабанного котла совместно с подводящими воду и отводящими пароводяную смесь трубами, с промежуточными коллекторами представляют собой систему, замкнутую на барабане или выносном циклоне и называемую контуром естественной циркуляции.
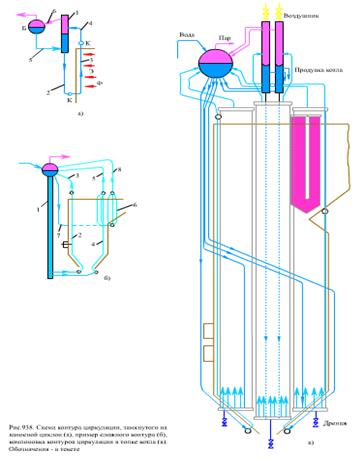
На рис.9.37 изображена схема простого контура циркуляции, приведены обозначения высот частей контура, используемые в расчете контура циркуляции. Высоту контура Нк принимают равной высоте опускных труб Нк = Ноп.

Простой контур циркуляции представляет собой систему последовательно включенных элементов (опускные, подъемные и отводящие трубы), каждый из которых выполнен из параллельно включенных труб, конструктивно тождественных и одинаково обогреваемых. Контур циркуляции, замкнутый на выносной циклон, показан на рис.9.38а.
Контур 1 - 2 - 3 - 4 простой, но циклон 1 дополнительно связан с барабаном системой водоподводящих 5 и пароотводящих 6 труб, влияющих на работу контура 1 - 2 - 3 - 4, и вся система барабан - 5 - 1 - 2 - 3 - 4 - 1 - 6 - барабан представляет собой сложный контур циркуляции. Этот сложный контур можно условно разделить на два простых - барабан - 5 - 1 - 6 и контур -1 - 2 - 3 – 4, имеющих общий элемент - циклон 1. Пример сложного контура представлен на рис.9.38б и включает в себя барабан, опускной стояк 1, к которому параллельно подключены подъемные 2 и отводящие 3 трубы фронтового экрана и подъемные 4 и отводящие 5 трубы заднего экрана. Там же изображен контур, состоящий из испарительных труб трехрядного конвективного пучка 6 со своими опускными 7 и отводящими 8 трубами. Каждый из трех рядов конвективного пучка выполнен из одинаковых по конфигурации труб с одинаковым обогревом, но между собой ряды отличаются по обогреву и конфигурации, т.е. их можно рассматривать как три подъемных элемента, включенных параллельно. Таким образом, сложный контур циркуляции содержит в себе параллельно включенные элементы, отличающиеся конструкцией и интенсивностью обогрева.
На рис.9.38в показан вариант компоновки контуров циркуляции в топочной камере котла.
Для расчета контура циркуляции используются основные уравнения, рассмотренные в гл.8: уравнения неразрывности, движения, энергии и состояния. При описании движения среды в замкнутом контуре эти уравнения можно упростить, придав им специфический вид, обусловленный конкретными начальными и граничными условиями.
Уравнение неразрывности для установившегося движения в трубе с постоянным сечением f выражается через массовую скорость ρw потока:
ρw = const.
Расход массы через n параллельных труб Gт, кг/с,
| Gт = ρwfn. | (9.92) |
В контуре циркуляции расход циркулирующей среды GЦ через последовательно включенные элементы одинаков. Для последовательных элементов уравнение неразрывности (уравнение сплошности) запишется в следующем виде
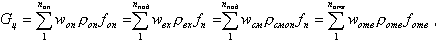
| (9.93) |
где индексы оп, под, отв, вх относятся соответственно, к опускным, подъемным, отводящим трубам и входному участку подъемных труб.
Одним из основных параметров, характеризующих работу контура, является скорость циркуляции w0, м/с
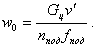
| (9.94) |
Задавшись w0, можно рассчитать скорость среды в других элементах контура, в частности в опускных трубах
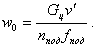
| (9.95) |
Уравнение движения для контура циркуляции запишем в виде суммы сопротивлений последовательно включенных элементов

| (9.96) |
Для каждого из элементов перепад давления определяется по известным формулам

где 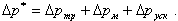
Для опускных, подъемных и пароотводящих труб можно рассчитать и построить гидравлические характеристики ∆p = f(w0) или Δp = f(GЦ) и, суммируя их, решить уравнение движения (9.96). При этом определяется скорость циркуляции w0 расход среды GЦ, количество образовавшегося пара GП и соответствующие им перепады давления по элементам контура циркуляции. По отношению GЦ и GП рассчитывается кратность циркуляции КЦ
| КЦ = GЦ/GП | (9.97) |
Уравнение движения можно представить и в другом виде - через движущий напор Sдв (см. § 8.5), который идет на преодоление сопротивлений трения, местного и ускорения в контуре
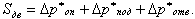
| (9.98) |
При расчете контура циркуляции по этому методу вводят понятие полезного напора циркуляции
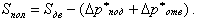
| (9.99) |
При расчете сопротивления 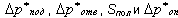 нивелирные напоры не учитываются.
нивелирные напоры не учитываются.
Из формулы (9.98) с учетом (9.99) получим простую форму записи уравнения движения
| Sпол = ∆p*под | (9.100) |
Следовательно, полезный напор Sпол представляет собой часть движущего напора Sдв, расходуемую на преодоление сопротивления . Для решения уравнения (9.100) необходимо определить 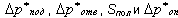 и Sдв. В итоге получим значения w0, GЦ, GП и KЦ.
и Sдв. В итоге получим значения w0, GЦ, GП и KЦ.
Оба метода решения уравнения движения будут рассмотрены ниже.
Уравнение энергии для установившегося движения потока в испарительных поверхностях топочной камеры будем использовать в виде уравнения теплового баланса
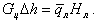
| (9.101) |
Уравнения состояния выражают зависимости теплофизических свойств водного теплоносителя от давления и температуры: ср, λ, v, ρ = f(p,t); с'p, λ', v', ρ'; с"p , λ", v", ρ" = f(p).
Начальные условия при рассмотрении стационарного движения потока в контуре циркуляции не задаются.
Граничные условия должны быть известны из конструктивного выполнения контура циркуляции, из теплового расчета котла, который проводится до расчета контура циркуляции. Если результаты расчета контура циркуляции покажут низкую надежность его работы, необходимо изменить конструктивное выполнение контура циркуляции, топочной камеры, тепловосприятие в топке и т.д. Эти изменения могут привести к необходимости выполнения нового теплового расчета котла.
Дата добавления: 2015-07-10; просмотров: 1820;
