Шумовые характеристики радиоприемников
Во всяком проводнике имеются свободные электроны, которые находятся в состоянии беспорядочного теплового движения подобно молекулам газа. В среднем достаточно большой промежуток времени распределение электронов по объему проводника можно считать равномерным. Однако вследствие беспорядочного теплового движения равномерность распределения электронов в отдельные моменты времени нарушается. При этом между концами проводника возникает ЭДС флуктуационного шума, которая беспорядочно изменяется во времени.
Теория флуктуаций показывает, что всякому комплексному сопротивлению Z=R+jX соответствует ЭДС флуктуационных шумов, эффективное значение которой Е определяется выражением
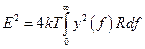 , (3. 1)
, (3. 1)
где k - постоянная Больцмана (1,38·10-23 Дж/град);
Т - абсолютная температура сопротивления;
R – активная составляющая сопротивления Z;
y( f ) - уравнение резонансной кривой цепи, которая соединяет сопротивление с прибором, измеряющим шум.
В большинстве случаев можно считать, что сопротивление R постоянно в широкой полосе частот, поэтому выражение можно представить в следующем виде
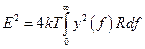 , (3.2)
, (3.2)
где В - энергетическая (шумовая) полоса пропускания приемника.
Как определяется энергетическая полоса пропускания на основании
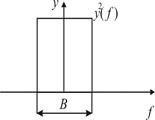 Рис. 3. 1
Рис. 3. 1
|
амплитудно-частотной характеристики резонансной цепи, видно из рисунка 3.1. Для этого на основании амплитуд-но-частотной характеристики строится зависимость y2(f). Затем определяется площадь под этой кривой и строится прямоугольник в этой системе координат, площадь которою равна площади под кривой
y2(f). Основание этого прямоугольника равно энергетической полосе данной цепи. Величина В обычно больше или равна полосе пропускания резонансной цепи на уровне 0,707. Чем ближе амплитудно-частотная характеристика к прямоугольной, тем лучше выполняется условие, что 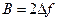 . Для одиночного колебательного контура справедливо равенство
. Для одиночного колебательного контура справедливо равенство 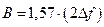 .
.
Реактивное сопротивление X в рассматриваемое сопротивление не входит, потому что оно обусловлено электрическими и магнитными полями, в которых отсутствуют флуктуации распределения электронов.
Обычно для расчетов принимают комнатную температуру Т = 300К. В этом случае ЭДС шумов определяется по простой формуле
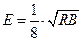 , (3.3)
, (3.3)
где Е - в мкВ, R - в кОм, В - в кГц.
Таким образом, шумящее сопротивление можно представить в виде следующей эквивалентной схемы:


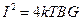
Рис. 3. 2
Для любой из этих схем можно определить номинальную мощность шумов. Под номинальной мощностью шумов понимается такая мощность, которая может быть отдана в согласованную нагрузку (R = Rн). Номинальная мощность шумов шумящего сопротивления определяется по формуле
|
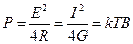
Как видно из полученного выражения номинальная мощность шумов не зависит от величины сопротивления.
Дата добавления: 2015-08-11; просмотров: 1848;
