Скорость и ускорение

Скорость - это отношение пройденного пути ко времени, за которое этот путь пройден.
Скорость так же - это сумма начальной скорости и ускорения умноженного на время.
Скорость - произведение угловой скорости на радиус окружности.

v=S/t
v=v₀+a*t
v=ωR

Ускорение тела, при равноускоренном движении - величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло.

a=(v-v₀)/t

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

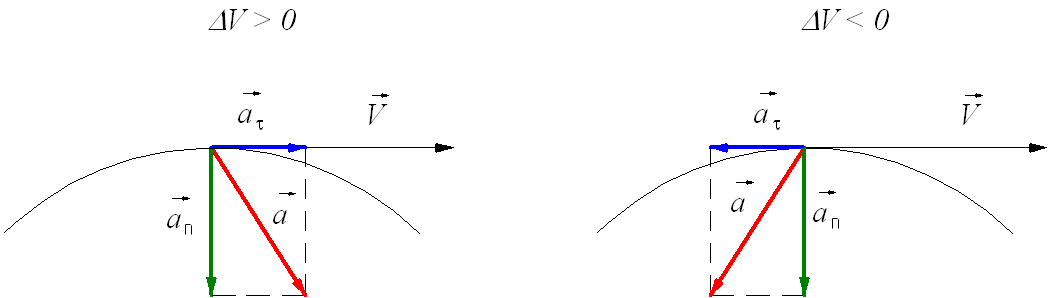
Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения 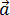_τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 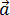_n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

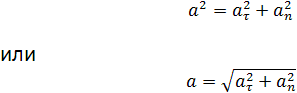
(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

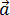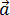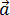= _τ + _n

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

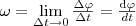
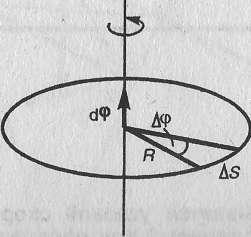
v=ωR

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

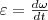
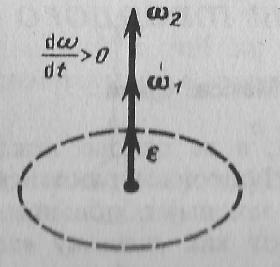
Рис.3

При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).

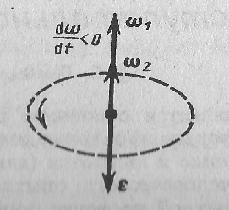
Рис.4

Тангенциальная составляющая ускорения a_τ=dv/dt , v = ωR и

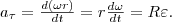
Нормальная составляющая ускорения

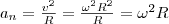
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

s = Rφ, v = Rω, а_τ = R?, a_n = ω²R.
В случае равнопеременного движения точки по окружности (ω=const)

ω = ω₀ ± ?t, φ = ω₀t ± ?t²/2,
где ω₀ — начальная угловая скорость.