Деформационные характеристики
Деформационные свойства грунтов необходимы при изучении закономерностей, связывающих деформации с напряжениями
Изучение деформируемости обычных материалов производится при одноосных испытаниях на растяжение и сжатие цилиндрических или призматических образцов. Для грунтов метод одноосных испытаний применим для образцов, способных удерживать заданную форму – тугопластичных глин.
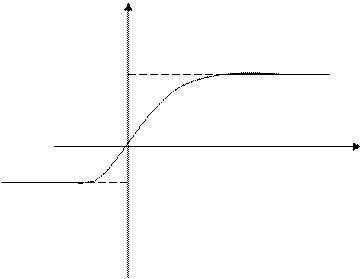
Результаты этих испытаний на растяжение и сжатие представлены на диаграмме (рис.1) из которых следует:
1. При небольших напряжениях связь между деформациями и напряжениями линейная.
2. На растяжение грунт работает значительно хуже, чем на сжатие.
3. грунт разрушается путем пластического течения с соответствующими площадками и пределами текучести.
Однако одноосные испытания не применимы для сухих песков или глинистых грунтов текучей консистенции и следовательно не универсальны.
 Ϭ
Ϭ
Текучесть при сжатии
Ϭ+т
Упругость
ε (отн. деформация)
Ϭ-т
Текучесть при
растяжении
Рис.3.2. Диаграмма испытаний на растяжение-сжатие для связного грунта.
Универсальным методом исследования деформационных свойств грунтов является компрессионный метод (К.Терцаги и др.).
Под компрессией понимается исследование сжимаемости грунтов без возможного бокового расширения. Испытания проводятся в компрессионных приборах, в которых грунт помещается в цилиндрическую обойму и в ней обжимается вертикальной нагрузкой через рычажную систему. Высота образца h=25мм, а площадь – 60см2. испытания образца грунта производят ступенчатым приложением нагрузки. Величина ступеней 0,65мПа.
Каждую ступень нагрузки выдерживают до затухания осадки (условной стабилизацией деформаций). Для каждой ступени нагружения с помощью индикатора часового типа измеряют абсолютную осадку S.
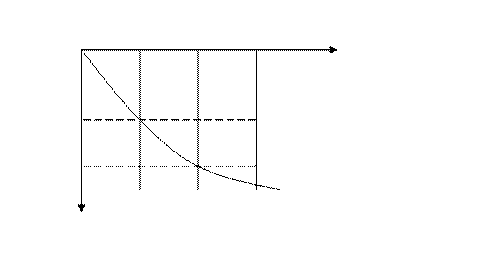
По результатам испытаний можно для каждой ступени вычислить относительную осевую деформацию ε=S/h и построить график зависимости ε=f(Ϭ). Такой график называется диаграммой сжатия (рис.2).
0 ΔϬ` Ϭ
mϑ Δε`
α ΔϬ``
Δε``
ΔϬ```
Δε```
ε
Рис. 3.3. Диаграмма сжатия ε=f(Ϭ)
Из графика видно, что связь между относительными деформациями и напряжениями нелинейная. В небольших интервалах напряжений нелинейную зависимость можно заменить линейными. Тангенс угла наклона спрямленного участка к оси Ϭ называется относительным коэффициентом сжимаемости и обозначается:
mϑ= Δε/ ΔϬ (3.1)
С использованием понятия относительного коэффициента сжимаемости mϑ, определяется для приращения модуль деформации Е
Е= (ΔϬ*β)/ Δε или Е= β/ mϑ (3.2)
При производственных испытаниях модуль деформации чаще всего определяют на участке изменения нагрузки Ϭ от 0,1 до 0,2мПа или для того диапазона напряжений, в котором ожидается работа основания сооружения.
Коэффициент β учитывает компрессионные условия сжатия грунта и зависит от коэффициента Пуассона ϑ – коэффициент бокового расширения
Β=1-(2ϑ2/(1-ϑ)) (3.3)
Пользуясь только компрессионными испытаниями, модуль деформации определить невозможно, так как неизвестен коэффициент β, зависящий от коэффициента Пуассона ϑ, который принимается по справочным данным в зависимости от вида грунта
Таблица 3.1.
| Вид грунта | Коэфф. Пуассона ϑ | β |
| Крупнообломочный | 0,27 | 0,80 |
| Пески, супеси | 0,30 | 0,74 |
| Суглинки | 0,35 | 0,62 |
| Глины | 0,42 | 0,39 |
Исходя из обобщенного закона Гука
ε=(Ϭi-2ν Ϭi)/Е= (Ϭi/Е)*(1-2) ν, ν=1/2[1-(Е*εi/ Ϭi)]
Принимая вертикальную ось Оz, где Ϭ=Ϭz, заметим боковые напряжения в силу симметрии равны Ϭx=Ϭy=Ϭδ. Тогда, из обособленного закона Гука при отсутствии боковых деформаций εδ=0 получим связь между вертикальным и боковым давлением:
Ϭδ= ν/(1-ν)*Ϭ= ξ*Ϭ, т.к. ε-кси
ξ = ν/(1- ν). (3.4)
Параметр ξ называется коэффициентом бокового давления грунта в состоянии покоя. Он определяется на компрессионном приборе при замене обычной обоймы на тензочувствительное кольцо, позволяющее изменить боковое давление на стенке Ϭδ= Ϭх= Ϭу где из выражения Ϭх=Ϭу=ν/(1- ν)*Ϭz можно найти коэффициент Пуассона.
Другой случай компрессионных испытаний по установлению основных показателей сжимаемости грунтов заключается в определении зависимости коэффициента пористости от напряжения е=f(Ϭ).
Как известно, сжимаемость дисперсных грунтов является их характернейшим свойством, отличающим грунты от массивных горных пород и других твердых тел. Она заключается в способности грунтов изменять свое строение (упаковку твердых частиц) под влиянием внешних воздействий (сжимающей нагрузки, высыхания, коагуляции коллоидов и пр.) на более компактное за счет уменьшения пористости.
Основным процессом изменения своего строения или объема грунта будет уплотнение под нагрузкой.
Зависимость коэффициента пористости от напряжения по результатам компрессионных испытаний выражается в форме графика, называемого компрессионной кривой.
Если обозначить:
ео- начальный коэффициент пористости грунта
еi- коэффициент пористости при любой степени нагрузки;
Si – полная осадка образца при данной нагрузке Ϭi, измеренная от начала загружения;
ΔVр=ΔV=Si*A – изменение объема пор от начала загружения;
Vs – объем твердых частиц (скелета) грунта;
А – площадь образца грунта;
h – начальная высота образца;
εi – относительная деформация при любой ступени нагрузки;
то учитывая, что коэффициент пористости есть отношение объема пор к объему скелета, будем иметь
еi=ео-ΔVо/Vs
Окончательно получим выражение
еi=ео-Si*A/Vs=eo- εi*(Vs+VPo)/Vs=eo- εi[1+VPo/Vs]
или
еi=eo- εi*(1+eo) (3.5)
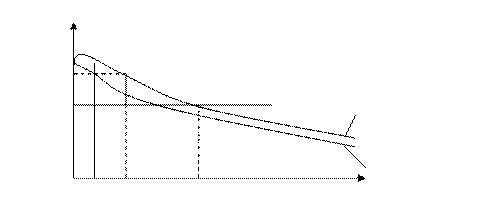
С помощью этой зависимости строим компрессионную кривую е=f(Ϭ) (рис 3.4.)
 е
е
ео
Δе 1
Ϭстр ΔϬ Ϭ, МПа
На рисунке в общем случае компрессионной кривой (линия 1) выделяются два участка.
На первом участке Ϭ<Ϭстр деформации грунта малы, т.к. при таком напряжении работают жесткие структурные связи.
При увеличении напряжений (на втором участке) Ϭ>Ϭстр структурные связи разрушаются и грунт начинает сильно уплотняться, т.е. изменяться коэффициент пористости. Величина Ϭстр называется структурной прочностью грунта.
Для грунтов, не имеющих жестких связей, первый участок отсутствует (линия 2).
По компрессионной кривой также можно оценить сжимаемость грунта. Она оценивается коэффициентом сжимаемости в определенных интервалах давления:
mo=|Δe|/ΔϬ=-Δe/ΔϬ (3.6)
Из рисунка видно, что чем круче компрессионная кривая, тем выше сжимаемость. В разных интервалах давления сжимаемость различная. Дифференцируя уравнение (3.6) получим:
de=-mo*dϬ (3.7)
Уравнение (3.7) называют дифференциальным законом уплотнения.
Этот закон формулируется следующим образом: бесконечно малое изменение относительного объема пор прямо пропорционально бесконечно малому изменению давления.
При небольших изменениях давлений уравнение (3.7) можно распространить и на конечные изменения величин е и Ϭ:
е1-е2=mo*(Ϭ2-Ϭ1)
Тогда закон уплотнения формулируется так: при небольших изменениях уплотняющих давлений изменение коэффициента пористости прямо пропорционально изменению давления (нагрузки).
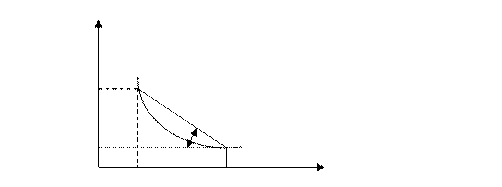
Руководствуясь законом уплотнения и повышением информативности компрессионной кривой, введено понятие коэффициента уплотнения грунта mo. Выражение сжимаемости грунта через коэффициент уплотнения представляет собой тангенс угла наклона к горизонту (рис), т.е.

 е
е
е1
mo
е2 α
0 Ϭ1 Ϭ2 Ϭ
Рис. 3.5. Спрямленная компрессионная кривая. (по Н.М. Герсеванову)
mo=tgα=(e1-e2)/ (Ϭ1-Ϭ2) (3.8)
В зависимости от коэффициента уплотнения mo степень сжимаемости может быть приблизительно охарактеризована следующим образом:
| Коэффициент уплотнения mo | Сжимаемость грунта |
| <0,001 | практически не сжимаемый |
| 0,001-0,005 | слабая |
| 0,005-0,01 | средняя |
| 0,01-0,1 | повышенная |
| >0,1 | сильная |
При фиксировании деформации сжатия S образца высотой h коэффициент пористости е может быть определен по зависимости
е=ео-(1-ео)*S/h (3.9)
Решая выражение (3.9) относительно ε=S/h принимая Ϭ2- Ϭ1= Ϭ получаем
S=mν*Ϭ*h (3.10)
mν- коэффициент относительной (объемной) сжимаемости связан с коэффициентом сжимаемости mo. Согласно этой связи, учитывая, что
Δε=-Δε*(1+ео):
mν= mo/(1+ео) (3.11)
Величина обратная mν представляет собой компрессионный модуль деформации, соответствующий изменению уплотняющего давления от Ϭ1 до Ϭ2 при изменений коэффициента пористости от е1 до е2. Поэтому модуль деформации можно выразить через коэффициент сжимаемости:
Е=β/mν=β*(1+ео)/ mo (3.12)
В расчетах по прогнозу осадки сооружений определяется модуль осадки (сжимаемости) ео (по Н.Н. Маслову). В качестве меры сжимаемости грунта используется величина относительной деформации ε=S/h.
При определении посредством опыта при нагрузке Ϭ устанавливают абсолютную величину сжатия S образца высотой h и в последующем вычисляют еϬ- модуль осадки равный относительной деформации
еϬ=ε=S/h, (3.13)
индекс Ϭ указывает на величину нагрузки, которой отвечает данное значение еϬ. Так как модуль осадки грунта отражает величину деформации, т.е. величину сжатия в мм столба грунта высотой 1м, когда к нему приложена дополнительная нагрузка Ϭ, то вместо формулы (3.13) будем иметь
еϬ=1000*S/h мм/м (3.14)
Отсюда, осадка S для случая одномерной задачи – S= еϬ*h.
Степень сжимаемости для разных категорий грунта по величине модуля осадки еϬ при Ϭ=3 кгс/см2 характеризуются следующими данными:
Таблица 3.2.
| Категория грунта по сжимаемости | Модуль осадки еϬ, мм/м | Сжимаемость |
| практически несжимаемый | ||
| I | 1-5 | слабая |
| II | 5-20 | средняя |
| III | 20-60 | повышенная |
| IV | >60 | сильная |
Просадочность грунтов. В отличии от осадки, которая подразумевает деформирование грунта по мере увеличения нагрузки, особенность просадочных грунтов является их способность давать дополнительные осадки при увлажнении даже при отсутствии внешней нагрузки.
Просадочность- это способность грунта уменьшатся в объеме при замачивании без увеличения нагрузки или при её отсутствии, т.е. только под действием собственного веса.
Величина предельно допустимой осадки для фундаментов составляет несколько сантиметров. Величина же просадок в просадочных грунтах при их значительной мощности достигает иногда 1-2м.
В сухом состоянии просадочные грунты являются хорошим основанием.
Пористость таких грунтов очень высокая – до 55… 65%, естественная влажность низкая 0,08… 0,16 при степени влажности Sr<0,5. агрегаты частиц соединены между собой водорастворимыми солями. Проникающая в грунт вода растворяет соли, переводя грунт в состояние жидкого коллоидного раствора, в результате чего грунт уплотняется. Таким образом, просадочные свойства обусловлены двумя факторами – высокой пористостью и наличием водонестойких связей в виде легкорастворимых солей (карбонатов).
Характеристика просадочности определяется по результатам испытаний образцов грунта ненарушенного сложения в компрессионных приборах и выполняется по одному из двух методов – метод одной кривой и метод двух кривых.
Метод одной кривой (рис 3.6.) применяют для определения относительной просадочности при одной заданной величине давления, равного суммарному давлению от собственной массы грунта в водонасыщенном состоянии и от проектируемого фундамента или только от массы грунта на глубине отбора образца.

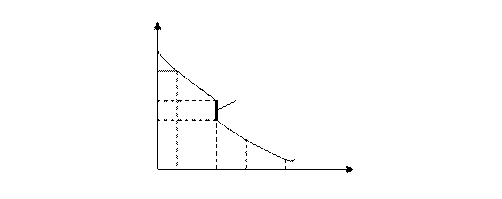
h
ho
hg
hp замачивание
hsl
Ϭzg 0,1 0,2 0,3 Ϭ
Рис. 3.6. Определение просадочности грунтов методом одной кривой.
После условий стабилизации осадки образца грунта на последней ступени задаваемого давления, образец грунта замачивается и исследуется до состояния его полного водонасыщения.
Метод двух кривых определяет относительную просадочность при различных давлениях (рис) при естественной влажности и после предварительного водонасыщения.
h
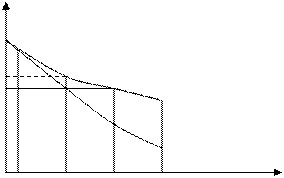
ho
 hγ 1
hγ 1
hp
 hsl 2
hsl 2
0 Ϭ 0,1 0,2 0,3 Ϭ
Рис. 3.7. Определение просадочности грунтов методом двух кривых: 1-для образца естественной влажности; 2-для водонасыщенного обрзца.
Просадочные свойства лессовых грунтов оцениваются двумя характеристиками: относительной просадочностью εsl и начальным просадочным давлением рsl.
Относительная просадочность определяется по формуле:
εsl=(hp-hsl)/ho,
где hp- высота образца природной влажности при давлении Ϭ;
hsl- высота образца при том же давлении после замачивания;
hо- начальная высота образца.
Грунт считается просадочным, если относительная просадка εsl≥0,01.
Начальное просадочное давление – это давление, при котором относительная просадочность εsl достигает значения 0,01.
Весьма важным показателем просадочности лессовых грунтов является их пористость. Степень просадочности сухих лессовых грунтов в зависимости от их пористости приводится в таблице
Таблица 3.8.
| Степень просадочности грунта | Пористость, n, % | Модуль просадочности, мм/м |
| непросадочные | ||
| слабопросадочные | 40-45 | |
| просадочные | 45-50 | |
| сильнопросадочные | 50-55 | |
| резкопросадочные | >55 | >100 |
Морозное пучение – это процесс увеличения объема грунта при его промерзании. Причина этого явления заключается в свойстве воды увеличиваться в объеме 9% при привращении её в лёд. Соответственно интенсивность морозного пучения грунта определяется количеством содержащейся в нем воды и степенью заполнения пор водой. Ориентировочные значения температуры конца пучения -3о…-5оС. Существенное влияние на величину морозного пучения оказывает миграция влаги в глинистых грунтах. Скорость миграции влаги пропорциональна градиенту температуры и влажности в грунте.
Для количественной оценки величины морозного пучения используется специальная характеристика – относительная деформация морозного пучения εfh:
εfh=hf/df,
где hf- вертикальная деформация образца грунта;
df- толщина промерзшего слоя образца.
В зависимости от величины εfh грунты поразделяются по степени пучинистости Таблица 3.8.
| Значение εfh | Характеристика пучинистости |
| εfh<0,01 | непучинистый |
| 0,01≤ εfh<0,04 | слабопучинистый |
| 0,04≤ εfh<0,07 | среднепучинистый |
| 0,07≤ εfh<0,1 | сильнопучинистый |
| εfh>0,1 | чрезмернопучинистый |
Пучению подвержены водонасыщенные глинистые грунты и пылевые пески (лёссы).
Другим специфическим свойством мерзлого грунта является его осадка при оттаивании.
Количественной оценкой осадки мерзлого грунта при оттаивании служит относительная осадка при оттаивании εth:
где hth- величина осадки образца мерзлого грунта высотой h при оттаивании.
Компрессионными испытаниями установлено, что величина относительной осадки εth зависит от действующего давления Ϭ. Эта величина может быть принята за линейную:
εth=Ath+mth*Ϭ,
где Ath- коэффициент оттаивания;
mth- коэффициент сжимаемости оттаивающего грунта.
Дата добавления: 2015-08-08; просмотров: 3013;
