Плоская задача. Действие равномерно распределенной нагрузки.

Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью 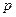показана на рис. 3.6.а.

Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:

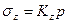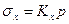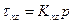; ; , (3.9)

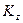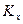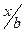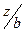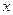где , , - коэффициенты влияния, зависящие от безразмерных параметров и ; и 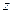– координатные точки, в которой определяются напряжения; 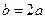– ширина полосы загружения.

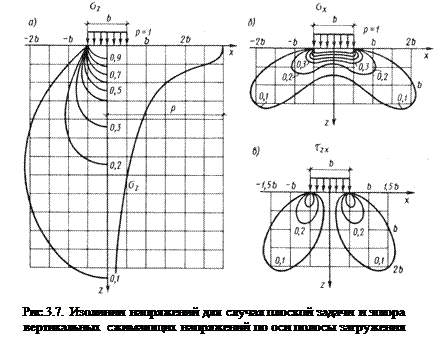
На рис. 3.7. а-в показано в виде изолиний распределение нарпряжени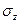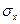и , и 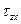в массиве грунте для случая плоской задачи.

В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:

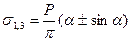, (3.10)

где 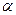- угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис.3.6.б).