Сокращение продольных размеров и замедление времени

Рассмотрим три важнейших следствия, которые вытекают из постулатов Эйнштейна, это равенство поперечных размеров движущихся тел в разных системах отсчета, замедление хода движущихся часов и сокращение продольных размеров движущихся тел, а затем обобщим полученные результаты в виде соответствующих формул преобразования координат и Рис.1.10.1

времени.

Пусть стержень AB движется относительно K-системы отсчета с постоянной скоростью V, параллельной длине стержня, (рис.1.10.1) и длина стержня равна l₀ в системе отсчета K’, связанной со стержнем.

Тогда можно показать, что искомая длина стержня в K-системе

(1.10.1)

где b = V/c. Длину l₀ измеренную в системе отсчета, где стержень неподвижен, называют собственной длиной.

Таким образом, продольный размер движущегося стержня оказывается меньше его собственной длины, т. е. l < l₀. Это явление называют лоренцевым сокращением. Заметим, что данное сокращение относится только к продольным размерам тел (размерам в направлении движения), поперечные же размеры не меняются. Сравнительно с формой тела в системе отсчета, где оно покоится, его форма в движущейся системе отсчета может характеризоваться как сплющенная в направлении движения.

Из формулы (1.10.1) следует, что степень сокращения зависит от скорости V. Эта зависимость особенно существенно проявляется для значений скорости V, сравнимой со скоростью света.

Итак, в разных инерциальных системах отсчета длина одного итого же стержня оказывается различной. Иными словами, длина — понятие относительное, имеющее смысл только по отношению к той или иной системе отсчета. Утверждение, что длина тела столько-то метров, не имеет смысла, пока не указано, к какой именно системе отсчета отнесена эта величина.

При малых же скоростях (V < c), как следует из (1.10.1), l » l₀ и длина тела приобретает практически абсолютный смысл.

Необходимо отметить, что лоренцево сокращение должно быть взаимным. Это значит, что если мы будем сравнивать два движущихся относительно друг друга стержня, собственная длина которых одинакова, то с «точки зрения» каждого из этих стержней длина другого стержня будет короче, причем в одинаковом отношении. Если бы это было не так, то имелась бы возможность экспериментально отличить инерциальные системы отсчета, связанные с этими стержнями, что, однако, противоречит принципу относительности.

Это говорит о том, что лоренцево сокращение является чисто кинематическим эффектом — в теле не возникает каких-либо напряжений, вызывающих деформацию.

Подчеркнем, что лоренцево сокращение тел в направлении их движения представляет собой реальный и объективный факт, отнюдь не связанный с какими-либо иллюзиями наблюдателя. Все значения размеров данного тела или промежутков времени, полученные в разных системах отсчета, являются равноправными (все они «правильные»). Трудность понимания этих утверждений связана исключительно с нашей привычкой, основанной на повседневном опыте, считать понятия длины и промежутков времени абсолютными понятиями, когда в действительности это не так. Понятия длины и промежутка времени столь же относительны, как понятия движения и покоя.

Наша следующая задача — сравнить течение времени в разных инерциальных системах отсчета. Как уже говорилось, время измеряется часами, причем под часами имеется в виду любой прибор, в котором используется тот или иной периодический процесс. Поэтому в теории относительности принято обычно говорить о сравнении хода идентичных часов в разных инерциальных системах отсчета.

.Пусть в K’-системе (рис1.10.1) часы неподвижны и их период 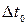. Обозначим период движущихся часов в K-системе 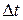.Соответствующие рассуждения дадут

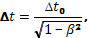(1.10.2)

где b = V/c, V — скорость часов в K-системе.

Отсюда видно, что 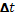> 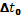, т. е. одни и те же часы в разных инерциальных системах отсчета идут по-разному: в той системе отсчета, относительно которой часы движутся, они идут медленнее, чем в системе отсчета, где они покоятся. Другими словами, движущиеся часы идут медленнее, чем покоящиеся. Это явление называют замедлением времени.

Время, отсчитываемое по часам, движущимся вместе с телом, в котором происходит какой-либо процесс, называют собственным временем этого тела. Его обозначают 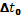. Как следует из (1.10.2), собственное время самое короткое. Время 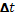того же процесса в другой системе отсчета зависит от скорости V этой системы относительно тела, в котором происходит процесс. Эта зависимость особенно сильно проявляется для значений скорости V, сравнимой со скоростью света

Таким образом, в отличие от ньютоновской механики течение времени в действительности зависит от состояния движения. Не существует единого мирового времени, и понятие промежуток времени между двумя данными событиями оказывается относительным. Утверждение, что между двумя данными событиями прошло столько-то секунд, приобретает смысл только тогда, когда указано, к какой системе отсчета это утверждение относится.

Абсолютное время ньютоновской механики является в теории относительности приближенным понятием, справедливым только при малых (по сравнению со скоростью света) относительных скоростях систем отсчета. Это сразу следует из (1.10.2): при V « c .

Итак, мы пришли к фундаментальному выводу: время в системе отсчета, движущейся с часами, течет медленнее (для наблюдателя, относительно которого данные часы движутся). Это относится и ко всем процессам, протекающим в движущихся относительно наблюдателя системах отсчета.

Естественно, возникает вопрос: заметит ли наблюдатель в K’-системе, движущейся относительно K‑системы, что его часы идут медленнее, чем часы K-системы? Нет, не заметит. Это сразу же следует из принципа относительности. Если бы K’-наблюдатель тоже обнаружил замедление времени в своей системе отсчета, то это означало бы, что для обоих наблюдателей — K’ и K время течет медленнее в одной из инерциальных систем отсчета. Из этого они заключили бы, что одна из инерциальных систем отсчета отличается от другой — в противоречии с принципом относительности.

Отсюда следует, что эффект замедления времени является взаимным, симметричным относительно обеих инерциальных систем отсчета K и K’. Иначе говоря, если с точки зрения K-системы медленнее идут часы K’-системы, то с точки зрения K’- системы, наоборот, медленнее идут часы K-системы (причем в том же отношении). Это обстоятельство указывает на то, что явление замедления времени является чисто кинематическим. Оно представляет собой обязательное следствие инвариантности скорости света и никак не может быть приписано какому-либо изменению в свойствах часов, обусловленному их движением.

Формула (1.10.2) сразу же нашла экспериментальное подтверждение, объяснив «загадочное» на первый взгляд поведение мюонов (микрочастиц) при прохождении земной атмосферы. Мюоны — это нестабильные частицы, которые самопроизвольно распадаются в среднем через 2·10^-6с (это время измерено в условиях, когда они неподвижны или движутся с малыми скоростями). Мюоны образуются в верхних слоях атмосферы на высоте 20—30 км. Если бы время жизни мюонов не зависело от их скорости, то, двигаясь даже со скоростью света, они не смогли бы проходить путь больше чем

c 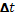= 3·10⁸ м/с · 2·10^-6 с = 600 м.

Однако наблюдения показывают, что значительное число мюонов все-таки достигает земной поверхности.

Это объясняется тем, что время 2·10^-6 с — это собственное время ( 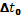) жизни мюонов, т. е. время по часам, движущимся вместе с мюонами. Время же по земным часам должно быть, согласно (1.10.2), гораздо больше (скорость этих частиц близка к скорости света) и оказывается достаточным, чтобы мюоны могли достигнуть поверхности Земли.

В заключение несколько слов о «парадоксе часов», или «парадоксе близнецов». Пусть имеются двое одинаковых часов A и B, из которых часы A неподвижны в некоторой инерциальной системе отсчета, а часы B сначала удаляются от часов A и затем возвращаются к ним. Предполагается, что в начальный момент, когда часы находились вместе, они показывали одно и то же время.

С «точки зрения» часов A движущимися являются часы B, поэтому они идут медленнее и по возвращении отстанут от часов A. С «точки же зрения» часов B, наоборот, движутся часы A, поэтому по возвращении отстанут именно они. Явное противоречие — в этом суть «парадокса».

В действительности в этих рассуждениях допущена принципиальная ошибка. Эта ошибка касается рассуждения с «точки зрения» часов B, так как система отсчета, связанная с этими часами, является неинерциальной (она сначала удаляется с ускорением, а затем приближается), и мы не имеем права в данном случае использовать результаты, относящиеся только к инерциальным системам отсчета. Детальный расчет, выходящий за рамки специальной теории относительности, показывает, что часы, движущиеся с ускорением (в нашем случае часы B), идут медленнее, поэтому при возвращении отстанут именно они.

Преобразования Лоренца.

Теперь нам предстоит решить фундаментальный вопрос о формулах преобразования координат и времени при переходе от одной инерциальной системы отсчета к другой (имеются в виду формулы, связывающие координаты и моменты времени одного и того же события в разных инерциальных системах отсчета).

Преобразования Галилея основаны на предположениях, что длина тел не зависит от движения и время течет одинаково в различных инерциальных системах отсчета. Однако в действительности это не так: течение времени и длина тел зависят от системы отсчета — выводы, являющиеся неизбежным следствием постулатов Эйнштейна. Поэтому мы вынуждены отказаться от преобразований Галилея, или, говоря точнее, признать, что они — лишь частный случай каких-то более общих преобразований.

Преобразования координат и времени, учитывающие изменения размеров и временных промежутков, называются преобразованиями Лоренца. Они при переходе от K- к K’-системе имеют вид:

(1.10.3)

а при обратном переходе от K’- к K-системе –

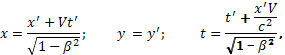(1.10.4)

где b = V/c, V — скорость K’-системы относительно K-системы, параллельная оси х. Следует сразу же обратить внимание на симметрию (одинаковый вид) формул (1.10.3) и (1.10.4), что является следствием полного равноправия обеих систем отсчета (различный знак при V в этих формулах обусловлен лишь противоположным направлением движения систем K и K’ относительно друг друга).

Преобразования Лоренца сильно отличаются от преобразований Галилея (1.3.1) и (1.3.2), однако последние могут быть получены из (1.10.3) и (1.10.4), если в них формально положить c = ¥. Что это значит?

В основе преобразований Галилея лежит допущение о синхронизации часов с помощью мгновенно распространяющихся сигналов. Из этого обстоятельства вытекает, что величина c в преобразованиях Лоренца играет роль скорости тех сигналов, которые используют для синхронизации часов. Если эта скорость бесконечно велика, то получаются преобразования Галилея; если же она равна скорости света, то — преобразования Лоренца. Таким образом, в основе преобразований Лоренца лежит допущение о синхронизации часов с помощью световых сигналов, имеющих предельную скорость.

Замечательной особенностью преобразований Лоренца является то, что при V « c они переходят в преобразования Галилея. Таким образом, в предельном случае V « c законы преобразования теории относительности и ньютоновской механики совпадают. Это означает, что теория относительности не отвергает преобразований Галилея как неправильные, но включает их в истинные законы преобразования как частный случай, справедливый при V « c. Это отражает общую взаимосвязь между теорией относительности и ньютоновской механикой — законы и соотношения теории относительности переходят в законы ньютоновской механики в предельном случае малых скоростей.

Далее, из преобразований Лоренца видно, что при V > c подкоренные выражения становятся отрицательными и формулы теряют физический смысл. Это соответствует тому факту, что движение тел со скоростью, большей скорости света в вакууме, невозможно. Нельзя даже пользоваться системой отсчета, движущейся со скоростью V = c; при этом подкоренные выражения обращаются в нуль и формулы также теряют физический смысл. Это значит, что, например, с фотоном, движущимся со скоростью c, принципиально не может быть связана система отсчета. Или иначе: не существует такой системы отсчета, в которой фотон был бы неподвижным.

И наконец, необходимо обратить внимание на то, что в формулы преобразования времени входит пространственная координата. Это важное обстоятельство указывает на неразрывную связь между пространством и временем. Другими словами, речь должна идти не отдельно о пространстве и времени, а о едином пространстве — времени, в котором протекают все физические явления.