Вращательное движение
Движение, при котором по крайнем мере точки твердого тела или неизменяемой системы остаются неподвижными, называемыми вращательным; прямая линия, соединяющая эти две точки, называется осью вращения.
Вращательное движение в технике встречается весьма часто. В подавляющем большинстве механизмов и машин имеются звенья, которые совершают вращательное движение, например, валы, зубчатые колеса, кривошипы и т.д. Заметим, что понятие вращательного движения может относиться только к телу, но не к точке; так, например, движение точки по окружности есть не вращательное движение, а криволинейное.
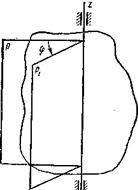
Если через ось вращения провести плоскость Р, жестко связанную с телом, то при вращении тела эта плоскость будет занимать новые положения (рис. 2.13). Угол между первоначальным положением плоскости Р и ее новым положением Р1 в текущий момент времени называется углом поворота тела и обозначается ср. Измеряется этот угол в радианах и считается положительным, если плоскость Р поворачивается против часовой стрелки (при этом надо смотреть с положительного конца оси z, направленной вдоль оси вращения тела). Кроме оси вращения для полного определения движения тела надо еще знать угол поворота φ как функцию времени t:φ=f(t) – закон вращательного движения тела. рис.2.13
Итак, при вращательном движении твердого тела точки его, находящиеся на различном расстоянии от оси вращения, имеют неодинаковые траектории, скорости и ускорения.
Отсюда следует, что линейное перемещение (путь), линейные скорость и ускорение точек не могут характеризовать вращательное движение тела в целом. Вращательное движение можно характеризовать углом φ, на который повернулось тело за данный промежуток времени. Этот угол называется угловым перемещением тела. Угловое перемещение выражается в радианах (рад) или оборотах (об); в последнем случае угловое перемещение обозначают N. Они связаны соотношением: φ =2πN (рад), N – число оборотов тела.
Путь любой точки вращающегося тела: s=rφ
Угловая скорость есть кинематическая мера движения вращающегося тела, характеризующая быстроту его углового перемещения: 
( рад/с)
Линейная скорость любой точки вращающего тела определяется формулой: υ=ωr, т. е. скорость точки прямо пропорциональна ее расстоянию от оси вращения.
В технике скорость вращения часто вращения оборотах в минуту, обозначают буквой п и называют частотой вращения. Угловая скорость и частота вращения, выраженные соответственно в рад/с и мин-1, связаны соотношением:
ω=πn/30 (рад/с)
Изменение угловой скорости во времени определяется уголковым ускорением ε = рад /с²: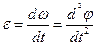 
Вектор углового ускорения направлен вдоль оси вращения, при вращения тела модуль угловой скорости может уменьшаться или увеличиваться. В первом случае вращения будет замедленным, а втором – ускоренным. При ускоренном движении направление вектора ускорения совпадает с направлением вектора скорости, а при замедленном – векторы скорости и ускорения будут направлены в разные стороны.
Равномерным вращением тела называется такое движение, при котором угловая скорость вращения тела остается постоянной. Если угловое ускорение тела постоянно, то такое вращение называется равнопеременным. Законы для равномерного и равнопеременного вращений получаются так же, как и аналогичные законы движения точки, поэтому при равномерном движении имеем: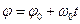 
, где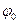 
- начальный угол поворота; 
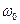- постоянная уголовая скорость тела.
Заменяя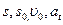 
в на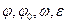 
, получим закон равнопеременного движения: 
.
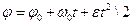Здесь 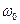— начальная угловая скорость. В любой момент времени угловая скорость будет определяться по формуле: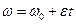 
Если при равнопеременном вращении скорость и ускорение направлены в одну сторону, то вращение называется равноускоренным и соответственно если направления скорости и ускорения не совпадают, то равнозамедленным.
Дата добавления: 2015-08-08; просмотров: 2642;