Интегралы движения системы М-точек
1) Импульс системы  ;
; 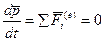 ,
, 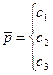 (13) для замкнутой системы М-точек, для которой
(13) для замкнутой системы М-точек, для которой 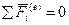 .
.
Имеем 3 интеграла движения для консервативных систем.
2) Момент импульса (механический момент) 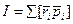 и
и 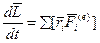 (19). Но для изотропного пространства, консервативной системы сумма моментов внешних сил
(19). Но для изотропного пространства, консервативной системы сумма моментов внешних сил  и
и 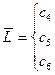 (20).
(20).
Еще 3 интеграла движения консервативной системы предполагает однородность времени и 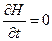 , а потому из (3) следует, что
, а потому из (3) следует, что
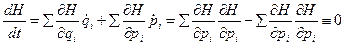 и
и 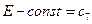 .
.
Теорема Э. Нетер: для нерелятивистских механических консервативных систем имеем 7 функционально независимых интегралов движения.
Лекции 7-8
Теорема Лиувилля и следствие из нее. Квантование в фазовом пространстве. Элемент фазовой протяженности. Статистический вес тела. Энтропия
 1. Теорема Лиувилля: элементы фазовых объемов dW0 и dW равны, если в dW перешли по фазовым траекториям фазовые точки из dW0 за время dt. Скорость «расползания» точек 1, 2 суть
1. Теорема Лиувилля: элементы фазовых объемов dW0 и dW равны, если в dW перешли по фазовым траекториям фазовые точки из dW0 за время dt. Скорость «расползания» точек 1, 2 суть  , скорость «расползания» точек 1, 4:
, скорость «расползания» точек 1, 4: 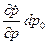 . Отрезки объема 1¢2¢3¢4¢
. Отрезки объема 1¢2¢3¢4¢  и
и 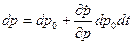 . Отбрасывая член с dt2, имеем
. Отбрасывая член с dt2, имеем  . Но скобка равна нулю в силу уравнений Гамильтона. Теорема доказана для n=1. Обобщаем на любое n. Имеем очевидное соотношение:
. Но скобка равна нулю в силу уравнений Гамильтона. Теорема доказана для n=1. Обобщаем на любое n. Имеем очевидное соотношение:
 (1). Но
(1). Но 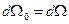 по теореме Лиувилля, т.е.
по теореме Лиувилля, т.е. 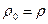 (2) в силу законов движения. Значит r - интеграл движения.
(2) в силу законов движения. Значит r - интеграл движения.
Легко подобрать условия (систему координат), чтобы два тела было 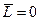 ,
, 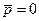 . Тогда по теореме Э. Нетер
. Тогда по теореме Э. Нетер
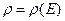 (3).
(3).
2. Статистическая теория в квантовом обобщении требует, чтобы 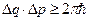 и поэтому на квантовое состояние в фазовом пространстве приходится элемент числа микросостояния (квазиклассическое приближение).
и поэтому на квантовое состояние в фазовом пространстве приходится элемент числа микросостояния (квазиклассическое приближение). 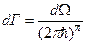 (4) в ситуации квазинепрерывности квантовых переходов.
(4) в ситуации квазинепрерывности квантовых переходов.
3. Статистический вес Г макроскопической системы. Энтропия. Полное число возможных при данных термодинамических условиях для тела число микросостояний называется статистическим весом системы Г. Это астрономически большое число. Поэтому вводим функцию
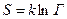 , (5) причем для того, чтобы сохранить размерность величины
, (5) причем для того, чтобы сохранить размерность величины 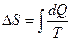 (термодинамическая энтропия), вводим множитель
(термодинамическая энтропия), вводим множитель  Дж/К. Функция (5) - энтропия в статистике. Ниже покажем, что она совпадает с энтропией в термодинамике.
Дж/К. Функция (5) - энтропия в статистике. Ниже покажем, что она совпадает с энтропией в термодинамике.
Лекции 9-10
Соотношения для средних по времени и по фазовому пространству. Связь между функциями r и S. Система в термостате. Функция распределения по Гиббсу. Постановка задачи
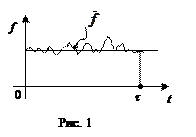 1. среднее значение физической величины f, которая зависит от времени через посредство q и p или явно оценивается как
1. среднее значение физической величины f, которая зависит от времени через посредство q и p или явно оценивается как
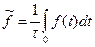 (1),
(1),
t - достаточно большой промежуток времени наблюдения. Расчет величины (1) нереален. Если воспользоваться постулатом Гиббса и распределением в фазовом пространстве, то 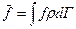 (2). Мы здесь вместо dW ввели элемент фазовой протяженности
(2). Мы здесь вместо dW ввели элемент фазовой протяженности 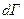 ~
~ 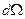 , причем
, причем 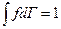 (3). Постулируем для консервативных механических систем (газ, жидкость, твердое тело), что
(3). Постулируем для консервативных механических систем (газ, жидкость, твердое тело), что 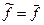 (3) и делаем возможным математическое решение проблемы о средних величинах в физике.
(3) и делаем возможным математическое решение проблемы о средних величинах в физике.
2. Свяжем Г и r, исходя из общей записи условия нормировки для функции r: 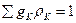 , где gK - число микросостояний для данного уровня энергии ЕК. Усредняем это условие:
, где gK - число микросостояний для данного уровня энергии ЕК. Усредняем это условие:
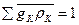 или
или 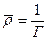 .
.
Поэтому 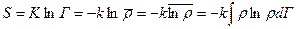 (4).
(4).
Мы здесь воспользовались свойством lnr линейно зависеть от энергии системы (см. ниже).
Для замкнутых систем с 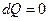 в необратимых процессах имеет место
в необратимых процессах имеет место 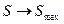 . Поэтому для отыскания равновесной функции распределения можно в соответствии со 2-м законом термодинамики потребовать
. Поэтому для отыскания равновесной функции распределения можно в соответствии со 2-м законом термодинамики потребовать 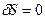 (5); из этого условия варьирования S находится в самом общем случае r.
(5); из этого условия варьирования S находится в самом общем случае r.
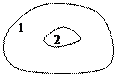 3. Пусть имеем систему 2, погруженную в термостат 1 (см. рис. 2). И система, и термостат находятся в состоянии теплового равновесия. Наша задача - найти функцию распределения r для системы 2 в этих условиях.
3. Пусть имеем систему 2, погруженную в термостат 1 (см. рис. 2). И система, и термостат находятся в состоянии теплового равновесия. Наша задача - найти функцию распределения r для системы 2 в этих условиях.
Можно записать для 1, 2 условия:
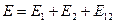 , (6)
, (6)
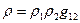 . (7)
. (7)
Здесь Е12 энергия взаимодействия 1 и 2, r - функция распределения для полной системы, g12 учитывает возможную корреляцию 1 и 2 за счет граничных эффектов.
Характерный размер 1 - L1, системы 2 - L2, толщина граничного слоя 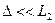 ,
, 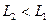 .
.
Лекция 11-12
Вывод функции распределения по Гиббсу. Свойства параметров функции Гиббса. Свободная энергия системы. Статистическая сумма.
1.Поскольку естественно допустить, что Е1~ 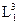 , Е2~
, Е2~ 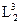 , а Е12~
, а Е12~ 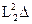 , ~ величинами Е12 в уравнении энергии
, ~ величинами Е12 в уравнении энергии
Е=Е1+Е2+Е12 (1)
Это возможно в силу короткодействующих межатомных сил. Можно пренебречь и коррелятор g12 в выражении
r=r1r2 g12 (2)
Оценка: 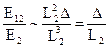 <<1, можно принять g12=1. В этом случае имеем систему функциональных уравнений:
<<1, можно принять g12=1. В этом случае имеем систему функциональных уравнений:
Е=Е1+Е2, (3)
r(E)=r1(E1)r2(E2) (4)
Последнее уравнение запишем в виде 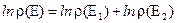 (5)
(5)
В (4-5) мы использовали теорему Лиувилля, т.е. возможность записать функцию распределения как функции энергии тела или его частей. Система уравнений (3)-(5) решается подстановкой Гиббса:
lnr(E)=aE+b (6)
причем a1=a2=…=a, b=b1+b2+… (7).
Тогда 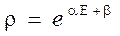 (8)
(8)
Легко показать, что должно иметь место a<0 и можно положить:
a= 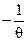 , b=
, b= 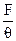 (9)
(9)
q - статистическая температура (q³0), F – свободная энергия тела.
Нормировка:  (10)
(10)
1. Из условия нормировки (10) легко находим:
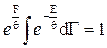 или F=
или F= 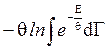 (11)
(11)
Интеграл 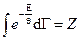 (12) называется статистической суммой для квазистатического случая квантовой механики.
(12) называется статистической суммой для квазистатического случая квантовой механики.
Строгое выражение нормировки имеет вид:
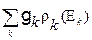 =1 (13)
=1 (13)
и, соответственно
Z= 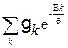 (14)
(14)
g12 – число микросостояний для уравнения энергии Еk. Уравнение Еk энергии находится из уравнения Шреденгера квантовой механики:
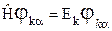 (15)
(15)
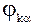 - волновые функции, a=1,…, gk ; Еk – уровни энергии системы.
- волновые функции, a=1,…, gk ; Еk – уровни энергии системы.
Лекция 13–14
Математический аппарат статистической физики
1) рассчитаем статистическую сумму, для простейшей системы, в которой нет взаимодействия: идеальный газ.
Мы имеем для идеального одноатомного газа:
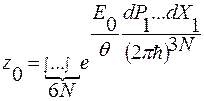 (1)
(1)
здесь проекция векторов импульса на оси координат  , а координаты частиц в объеме
, а координаты частиц в объеме 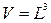 суть:
суть: 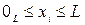 , i=1,…,3N. Имеем:
, i=1,…,3N. Имеем:
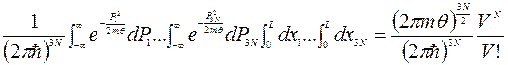 (2)
(2)
В знаменателе (2) учтено то обстоятельство, что при интегрировании по Xi в координатных интегралах можно интегрировать и по тем точкам, где находятся частицы. Повторы устраняются делением на число перестановок з N частиц, т.е. N!.
Рассчитаем теперь Z для гармонического осциллятора, т.к. связь между атомами в кристаллах модно моделировать таким образом. Расчет проведем учитывая возможную дискретность квантовых состояний, т.е. для соседних уравнений энергия ΔE может быть сопоставима с 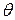 . Расчет проводится на основе
. Расчет проводится на основе 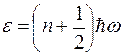 , n=1,2,3,…(3)
, n=1,2,3,…(3)
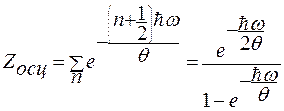 (4)
(4)
Используется известная формула суммы геометрической прогрессии, у которой знаменатель 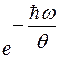 .
.
2) Теорема Гиббса–Гемгольца: 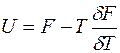 (5)
(5)
Для получения этого выражения дифференцируем условие нормировки по 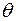 для функции ρ:
для функции ρ: 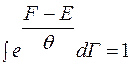 (6)
(6)
3) Уравнение состояния тела находим таким же способом. Производную от левой и правой части (6) берем как по параметру по V, причем учитываем, что Pмикро, создаваемое частицами тела на уровне микропроцессов 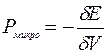 (7)
(7)
Тогда из (6) легко получаем 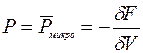 (8)
(8)
4) Энергия тела 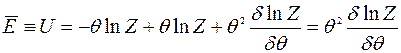 (9)
(9)
5) Основное термодинамическое тождество: мы его получим из условия 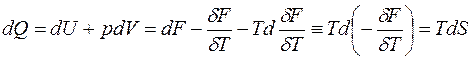 , (10)
, (10)
где  – термодинамическая энтропия.
– термодинамическая энтропия.
Отметим возможность одночастного распределения: распределением Больцмана.
Для идеального газа (в широком понимании этого слова)
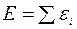 ,
, 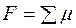 (
(  – химический потенциал) и
– химический потенциал) и 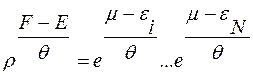 (11)
(11)
Отсюда следует, что распределение для отдельной частицы газа суть 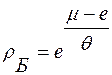 и нормировка
и нормировка  (12)
(12)
Дата добавления: 2015-08-08; просмотров: 838;
