Газовые законы. Если разрешить уравнение состояния идеального газа

Если разрешить уравнение состояния идеального газа

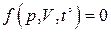
относительно какого-либо из параметров, например, p, то уравнение состояния примет вид

.

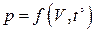И известные из школьного курса физики законы Бойля-Мариотта и Гей-Люссака дают уравнения состояния для случаев, когда один параметров остается постоянным.

Известные газовые законы (Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро) были открыты опытным путем задолго до появления молекулярно-кинетической теории. Эти законы были установлены на опытах с газами, находящимися в условиях, не очень сильно отличающихся от нормальных атмосферных условий, т.е. при не очень низких температурах и не очень высоких давлениях. При иных условиях экспериментальные газовые законы уже не точно отражают свойства газов, т.е. все эти законы являются приближенными.

Рассмотрим некоторые из этих законов:

1) Закон Бойля-Мариотта (m = const, T = const).

Изучая изотермические процессы, английский ученый Бойль (1662г.) и французский ученый Мариотт (1667г.) независимо друг от друга установили следующий закон:

ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянной температуре (T = const) давление газа изменяется обратно пропорционально объему.

Аналитически это можно записать в виде: P·V = const (T = const). Совокупность состояний, отвечающих одной и той же температуре, изобразится на диаграмме (P, V) кривой, определяемой уравнением гиперболы. Каждому значению температуры соответствует своя кривая, называемая изотермой. А переход газа из одного состояния в другой, совершающийся при постоянной температуре, называется изотермическим процессом.

2) Закон Гей-Люссака (m = const, P = const).

Изучая изобарические газовые процессы, французский физик Гей-Люссак в 1802г. установил следующий закон:

ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянном давлении объем газа меняется линейно с ростом температуры:
,
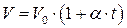где V – объем газа при температуре t°;
V₀ – объем газа при 0°C;
a – термический коэффициент объемного расширения ( ).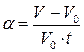

Термический коэффициент объемного расширения показывает, на какую часть относительно первоначального объема изменится объем газа при его нагреве на 1°. Для большинства газов .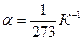

Процесс, протекающий при постоянном давлении, называется изобарическим. Для газа такой процесс отобразится на диаграмме (V, t°) прямой; здесь различные прямые отвечают разным давлениям и называются изобарами.

3) Закон Шарля (m = const, V = const).

ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянном объеме давление газа изменяется линейно с ростом температуры:
,
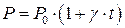где P – давление газа при температуре t°;
P₀ – давление газа при 0°C;
g – термический коэффициент давления газа ( ).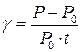

Аналогично сказанному ранее относительно коэффициента “a”, термический коэффициент давления газа показывает, на какую часть относительно первоначального давления изменится давление газа при его нагревании на 1°С.

Для идеального газа также 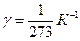. Для идеального газа .

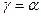Изохорический процесс, т.е. процесс, протекающий при постоянном объеме на диаграмме (P, t°) изобразится прямой линией. Различные прямые соответствую различным объемам и называются изохорами.

Заметим теперь, что все изобары и изохоры пересекают ось t° в одной и той же точке, определяемой из условия 1+a×t°=0. Откуда .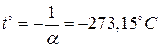

Если за начало отсчета температуры взять нуль (как это и было), то получим шкалу температур по Цельсию. Если сместить начало отсчета в точку -273.15, то перейдем к другой температурной шкале, которая называется абсолютной (или шкалой Кельвина).

В соответствии с определением абсолютной шкалы между абсолютной температурой (Т) и температурой по Цельсию (t) существует следующее соотношение:

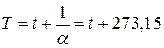. (9.1)

Температура равная 0°К называется абсолютным нулем.

Для установления абсолютной шкалы температур и абсолютного нуля мы воспользовались законами Гей-Люссака и Шарля и поступили сугубо формально. Однако Кельвин в 1852г., исходя из иных физических соображений установил такую же абсолютную шкалу температур с тем же значением абсолютного нуля, какие ранее были получены формально. Поэтому понятия абсолютной температуры и абсолютного нуля не следует рассматривать как формальные, не имеющие физического смысла. Кельвин показал, что абсолютный нуль – это самая низкая из возможных температур вещества. При абсолютном нуле прекращается хаотическое движение молекул в веществе. Однако это не означает, что в нем прекращается всякое движение. Сохраняется, например, движение электронов в атоме. В настоящее время удается охлаждать малые объемы вещества до температуры очень близкой к абсолютному нулю, не достигая последнего лишь на несколько тысячных долей градуса.

Перейдем теперь в уравнениях, описывающих законы Гей-Люссака и Шарля от температуры по Цельсию к абсолютной температуре, подставив вместо t величину .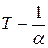

Тогда

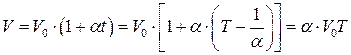. (9.2)

и аналогично

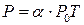(при условии g=a).

Из этих уравнений следует, что

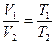
	(P = const)	(9.3)
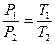
	(V = const)	(9.4)

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной и той же изобаре (для уравнения (9.3)), или одной и той же изохоре (для уравнения (9.4)).

Итак, при постоянном давлении объем газа пропорционален абсолютной температуре; и при постоянном объеме давление газа пропорционально абсолютной температуре.

Всякий реальный газ тем точнее следует уравнениям PV = const, 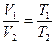, , 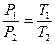чем меньше его плотность, т.е., чем больший объем он занимает.

В соответствии с уравнением PV = const, объем растет с уменьшением давления, а согласно с 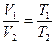объем возрастает с температурой. Следовательно, рассмотренные газовые законы справедливы при не слишком низких температурах и невысоких давлениях.

Газ, который точно следует этим уравнениям, называется идеальным. Всякий реальный газ по мере убывания его плотности приближается к идеальному.

Замечание:

1. Закон Дальтона.

ОПРЕДЕЛЕНИЕ: Парциальным давлением газа, входящего в газовую смесь, называется то давление, которое имел бы этот газ, если бы все остальные газы были удалены из объема.

В 1801гю английский физик и химик Дальтон установил соотношение между давлением газовой смеси и парциальными давлениями входящих в нее газов.

ОПРЕДЕЛЕНИЕ: Давление газовой смеси равно сумме парциальных давлений входящих в нее газов.

P=P₁+P₂+P₃+…