Ток за контуром
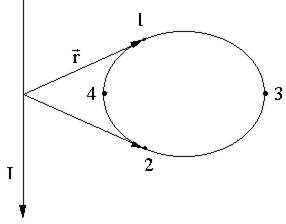
| При обходе контура 1 через 3 к 2 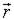 поворачивается по часовой стрелке, от 2 к 1 через 4 - на тот же угол против часовой стрелки. В результате
|
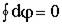
11.5.4. Формулировка теоремы о циркуляции
Пусть контур произвольной формы охватывает произвольное число токов. В этом случае теорема о циркуляции утверждает, что циркуляция вектора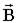 
по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
.
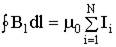Например:
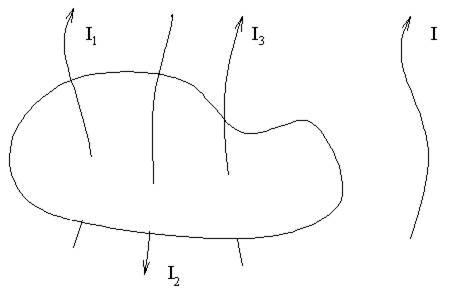
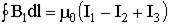
Ток I4 в сумму не входит!
11.5.5. Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида
Соленоид - провод, навитый на цилиндрический каркас. На один метр длины - n витков.
Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор 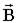может быть направлен только вдоль оси соленоида.
Тогда
.
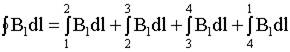1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1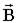 
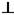стороне контура, значит Вl = 0.
2) Тогда:
.
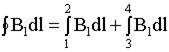3) Можно показать, что вне бесконечного соленоида B=0, т.е.
.
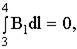Значит:
,
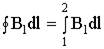т.к. внутри соленоида B = Bl = const, то
.
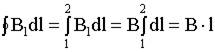По теореме о циркуляции (11.5.4)
.
Откуда магнитное поле бесконечного соленоида:
.
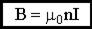Направлено 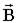вдоль оси соленоида, в соответствии с правилом правого винта.
Дата добавления: 2015-08-08; просмотров: 537;