Давление идеального газа

Самой простой моделью макроскопического вещества является газ частиц. Газ представляет собой достаточно разреженную систему частиц. Частицы в газе находятся на значительном удалении друг от друга, совершая свободное движение и время от времени сталкиваясь друг с другом. Поэтому в первом приближении при рассмотрении газа можно не учитывать размеры и форму молекул, т. е. считать частицы материальными точками. По этой же причине можно пренебречь взаимодействием частиц на расстоянии, и к столкновениям частиц между собой и со стенками сосуда применять законы соударений упругих шаров. Такой газ называется идеальным. Модель идеального газа позволяет описать существенные черты поведения реального вещества.

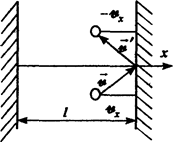Пусть в прямоугольном сосуде находится N молекул идеального газ». Стенки сосуда будем считать «идеально, отражающими». Примем,что при отражении от стенки скорость молекулы не меняется по величине, но меняется лишь по направлению. Если молекула, компонента скорости которой в направлении оси x равна v_x, ударяется о стенку, то после отражения компонента ее скорости в этом направлении будет ‑v_x.

Для изменения импульса в этом же направлении имеем Dp_x = 2·m·v_x.

Долетев до противоположной стенки, молекула отразится от нее и снова ударится о первую стенку. Время между ударами составит Δt = 2·l/v_x, а число ударов за 1 с будет 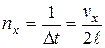. За 1 с молекула сообщит стенке импульс с компонентой вдоль оси x

.

Но импульс, передаваемый за единицу времени стенке, равен силе, с которой данная молекула действует на стенку. Таким образом, i-я молекула действует на стенку с силой, компонента которой в направлении оси x F_ix = mv²_ix/l.

Компонента силы, действующей вдоль оси x со стороны всех частиц, находящихся в сосуде, составит .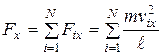

Перепишем это соотношение в виде .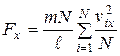

Величина 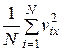есть средний квадрат компоненты скорости молекулы в направлении оси x. Поэтому 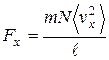. Если эту силу разделить на площадь стенки S, то получим величину давления на стенку:

. (2.5)

Но l·S есть объем сосуда V. Значит: .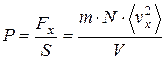

Таким образом, давление газа на стенку оказалось связанным со средним квадратом скорости смещения частиц в направлении нормали к стенке.

Воспользуемся теперь соотношением v²_i = v²_ix + v²_iy + v²_iz.

Усредняя его по всем частицам, получим <v²> = <v²_x>+ <v²_y>+ <v²_z>.

Но все направления в пространстве равноправны, поэтому <v²_x>= <v²_y>= <v²_z> и, следовательно, <v²_x>= <v²>/3. Выражение для давления принимает вид

.

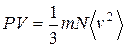Учтем, что величина m<v²>/2 равна средней кинетической энергии поступательного движения молекул <E_k>. Окончательно получим:

. (2.6)

Это соотношение одно из основных в кинетической теории газов.