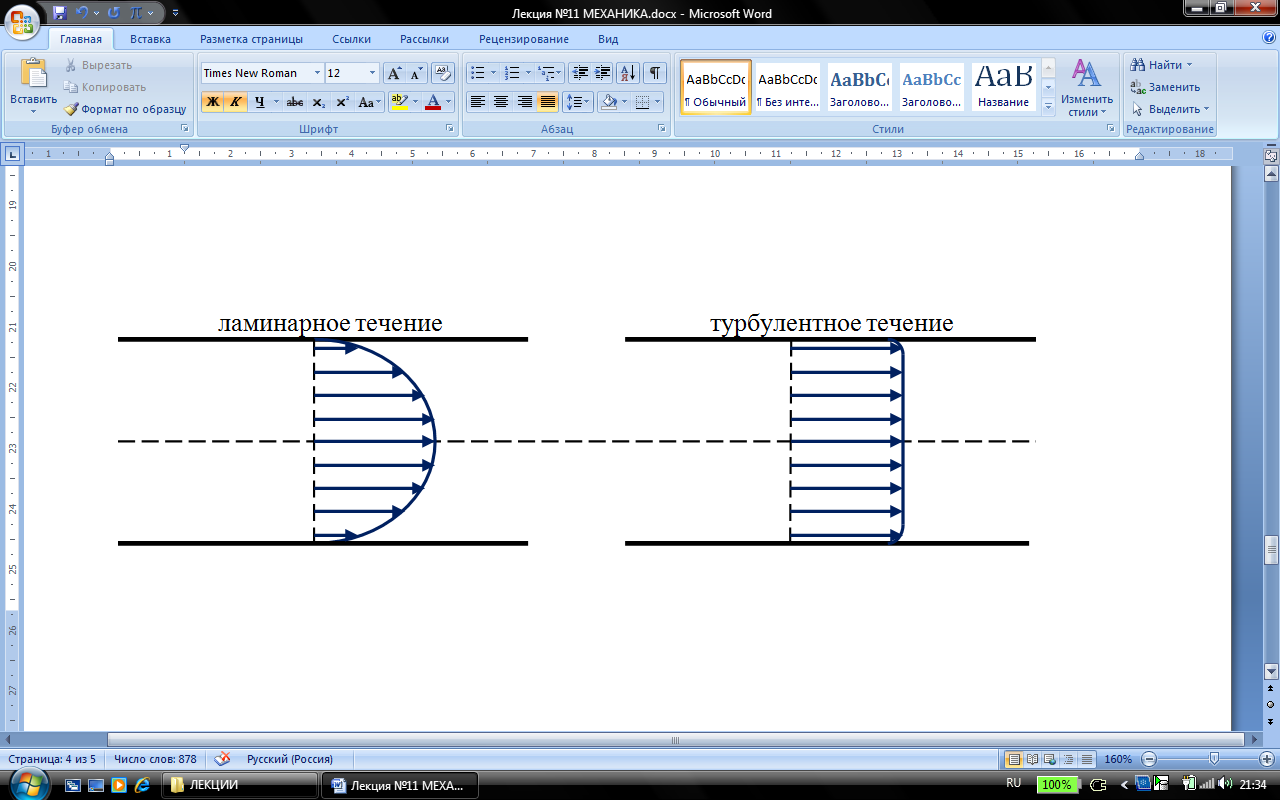
При ламинарном течении модуль скорости изменяется с расстоянием от оси трубы по параболическому закону.

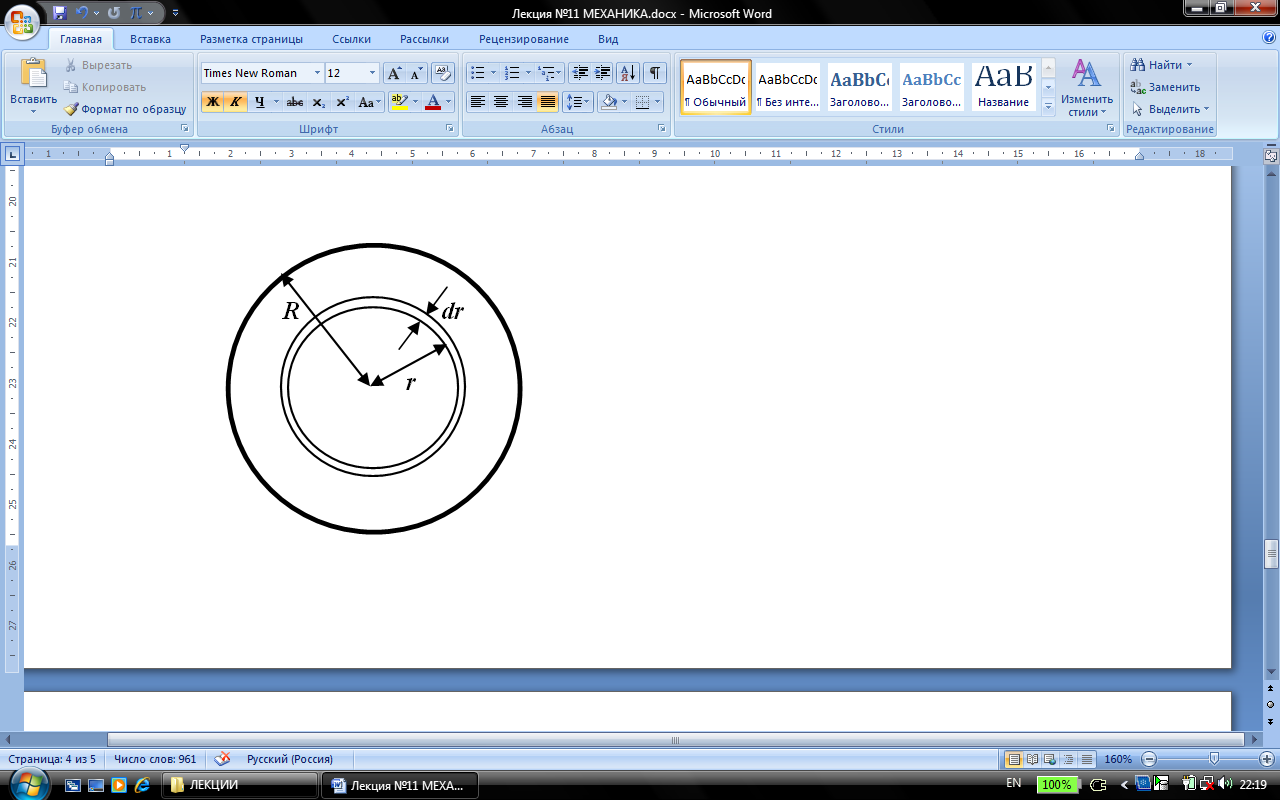Вычислим поток жидкости Q (объём жидкости), протекающий через поперечное сечение трубы в единицу времени. Выделим слой радиусом r и толщиной dr. Через него поток жидкости . Поток жидкости Q определяется интегрированием:

,

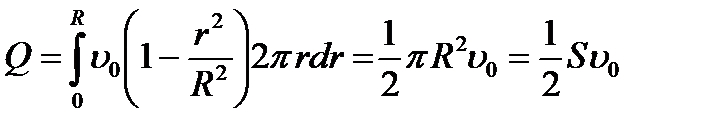где S – площадь сечения трубы. После подстановки в эту формулу :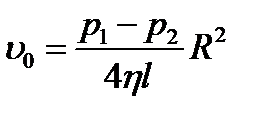

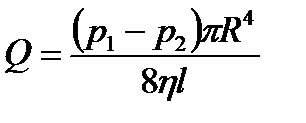– формула Пуазейля.

В случае нестационарного течения скорость частиц в каждой точке пространства всё время беспорядочно изменяется. Такое течение называется турбулентным. При турбулентном течении происходит интенсивное перемешивание жидкости.

Осборн Рейнольдс (английский физик 1842-1912 гг.) установил, что характер течения определяется значением безразмерной величины

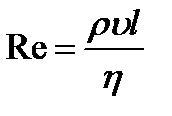– число Рейнольдса,

где ρ – плотность жидкости или газа, υ – средняя по сечению трубы скорость потока, η – вязкость жидкости или газа, l – характерный для поперечного сечения потока размер.

При малых значениях Re течение носит ламинарный характер. Начиная с критического значения Re, течение становится турбулентным. Для трубы .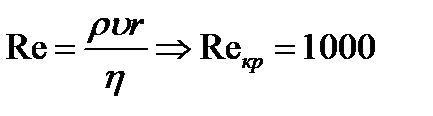

Величину 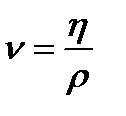называют кинематической вязкостью. С учётом этого .

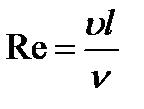При выяснении сил, действующих на тело, безразлично, что считать движущимся – тело или среду. Удобно предполагать тело неподвижным, а среду движущейся.

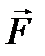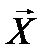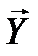Силу , с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скорости невозмущённого потока силу , называемую лобовым сопротивлением, и перпендикулярную к силу , называемую подъёмной силой. На тело, симметричное относительно направления скорости , может действовать только сила лобового сопротивления, подъёмная же сила будет отсутствовать.

Подъёмная сила крыла самолёта:

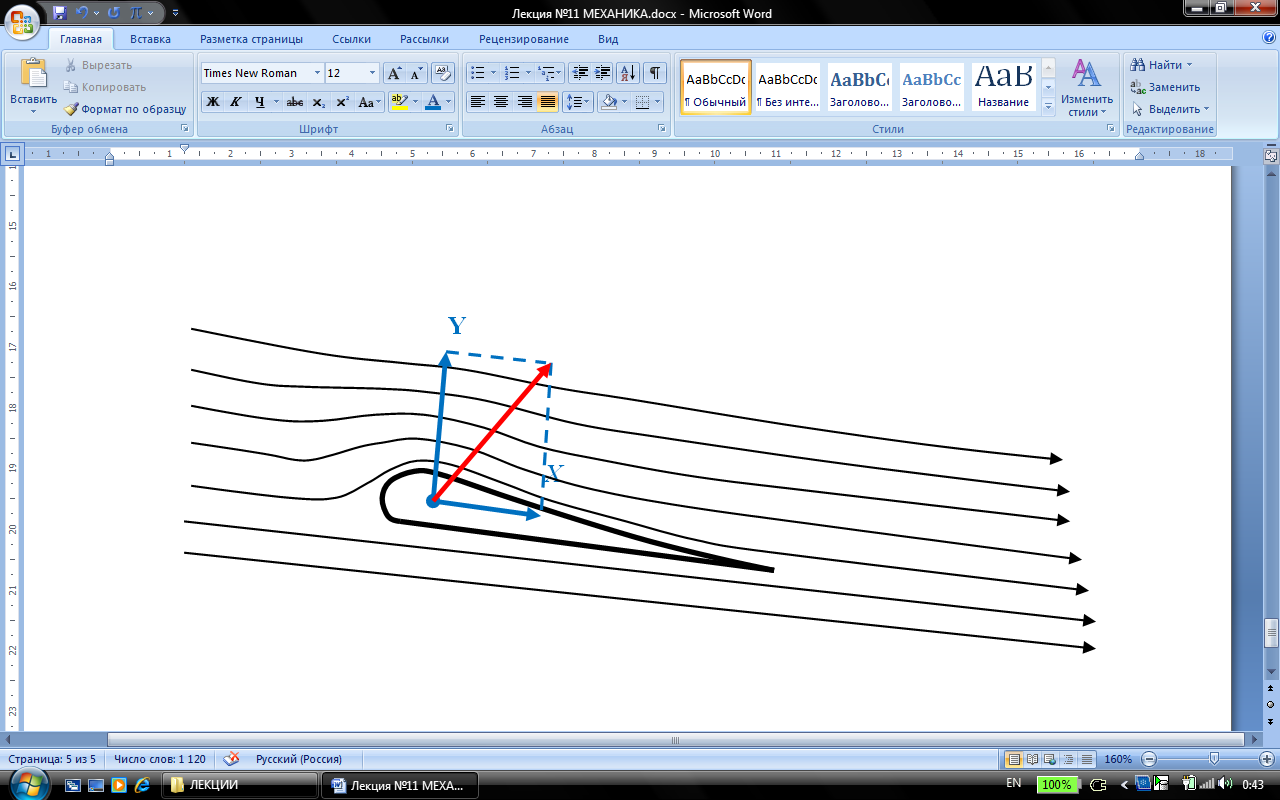
В несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления (парадокс Даламбера).

Стокс (Джордж Габриэль Стокс 1819-1903 гг. – английский физик и математик) установил, что при небольших скоростях и размерах тел (при малых Re) модуль силы сопротивления определяется формулой 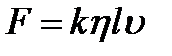, где η – динамическая вязкость, l – характерный размер тела, υ – модуль скорости тела, k – коэффициент пропорциональности, зависящий от формы тела.

Модуль силы сопротивления, действующей на небольшие шарики, движущиеся в жидкости, при малых скоростях определяется формулой:

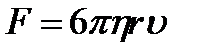- формула Стокса,

где r – радиус шарика.