Теоретический метод
Для теоретического метода определения коэффициента чувствительности требуется выбрать наиболее достоверное уравнение диаграммы предельных амплитуд и корреляционное соотношение между пределом выносливости при симметричном цикле и пределом прочности материала [15].
Связь между пределом выносливости и пределом прочности металлических конструкционных материалов, как уже частично отмечалось ранее, обычно представляют одним из следующих трех уравнений ( 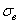 в МПа):
в МПа):
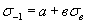 , (2.68)
, (2.68)
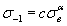 , (2.69)
, (2.69)
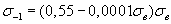 . (2.70)
. (2.70)
Параметры уравнений (2.68) и (2.69), найденные путем статистического анализа больших по объему совокупностей (нескольких сотен на вариант) экспериментальных данных представлены в табл. 2.4. Уравнение (2.70) рекомендуется стандартом [14] только для сталей.
Все уравнения (2.68)...(2.70) для соответствующих групп материалов приводят к близким результатам, однако предпочтение следует отдавать формуле (2.69), так как она не противоречит, в отличие от (2.68), граничным условиям и, как показал анализ, обеспечивает наибольшую точность оценки предела выносливости [1, 5, 6, 12].
Таблица 2.4. Значения параметров уравнений (2.68) и (2.69) для базы Nб = 107 циклов при переменном растяжении-сжатии
| Материал | a | b | с | 
| Источник |
| Углеродистые стали | 33,5 | 0,379 | 1,13 | 0,850 | [5] |
| Легированные стали | 0,329 | 2,02 | 0,777 | [5] | |
| Общая совокупность сталей | 69,2 | 0,354 | 1,60 | 0,820 | [5] |
| Титановые сплавы | 56,5 | 0,347 | 1,29 | 0,831 | [6] |
| Алюминиевые сплавы | 76,6 | 0,175 | 3,33 | 0,630 | [1, 5, 10, 11, 12] |
Как уже отмечалось ранее, существует достаточно широкий круг уравнений для диаграмм предельных амплитуд цикла напряжений, в соответствии с которыми получаются различные формулы для теоретического расчета коэффициента чувствительности материала к асимметрии нагружения  .
.
Эти формулы, наряду с широко используемыми в расчетной практике уравнениями диаграмм предельных амплитуд цикла напряжений, приведены в таблице 2.5.
Совместные решения уравнений (2.71).(2.74) с одним из уравнений (2.68)...(2.70) открывает возможность теоретической (расчетной) оценки коэффициента чувствительности материала к асимметрии цикла напряжений [15].
Таблица 2.5. Формулы для вычисления  на базе различных уравнений диаграмм предельных амплитуд
на базе различных уравнений диаграмм предельных амплитуд
| Уравнение диаграммы предельных амплитуд (автор) | Номер формулы | Формула для вычисления коэффициента 
| Номер формулы |
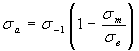 (Гудман) (Гудман)
| 1.8 | 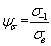
| 2.71 |
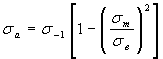 (Гербер) (Гербер)
| 1.9 | 
| 2.72 |
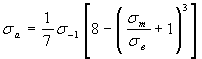 (Петерсон) (Петерсон)
| 1.11 | 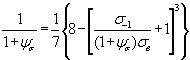
| 2.73 |
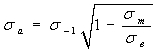 (Биргер) (Биргер)
| 1.12 | 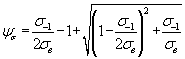
| 2.74 |
В качестве примере на рис. 2.10 для сталей показана зависимость коэффициента  , рассчитанного по формулам (2.71)...(2.74) с использованием уравнения (2.69), от уровня статической прочности.
, рассчитанного по формулам (2.71)...(2.74) с использованием уравнения (2.69), от уровня статической прочности.
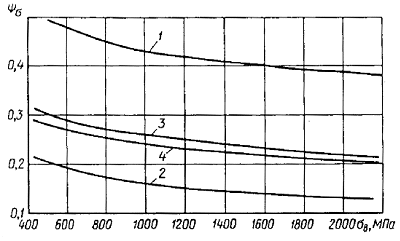
Рис. 2.10. Расчетные значения коэффициента  для сталей: 1, 2, 3, 4 – расчет по уравнениям (2.71), (2.72), (2.73), (2.74) соответственно
для сталей: 1, 2, 3, 4 – расчет по уравнениям (2.71), (2.72), (2.73), (2.74) соответственно
Для легированных и углеродистых сталей приведенные графики практически совпадают, поэтому здесь и далее для этих групп сталей будут приводиться осредненные данные.
Как видно из рис.2.10, величина коэффициента чувствительности  монотонно убывает с увеличением статической прочности сталей для всех видов используемых уравнений диаграммы предельных амплитуд (1.8), (1.9), (1.11), (1.12), что соответствует экспериментальным данным, представленным на рис.2.8, и противоречит уравнению (2.65), рекомендуемому стандартом [14]. Причем, как и следовало ожидать, выбор уравнения, связывающего предел выносливости материала с пределом прочности, не имеет сколько-нибудь значимого влияния. Для иллюстрации этого на рис. 2.11 приведены зависимости величины коэффициента чувствительности
монотонно убывает с увеличением статической прочности сталей для всех видов используемых уравнений диаграммы предельных амплитуд (1.8), (1.9), (1.11), (1.12), что соответствует экспериментальным данным, представленным на рис.2.8, и противоречит уравнению (2.65), рекомендуемому стандартом [14]. Причем, как и следовало ожидать, выбор уравнения, связывающего предел выносливости материала с пределом прочности, не имеет сколько-нибудь значимого влияния. Для иллюстрации этого на рис. 2.11 приведены зависимости величины коэффициента чувствительности  от предела прочности сталей, причем для расчета
от предела прочности сталей, причем для расчета  использовались все уравнения (2.68)...(2.70).
использовались все уравнения (2.68)...(2.70).
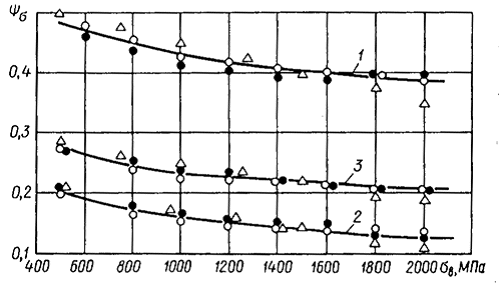
Рис.2.11. Расчетные значения коэффициента  для сталей: 1,2,3– расчет по уравнениям (2.71), (2.72), (2.74) соответственно,
для сталей: 1,2,3– расчет по уравнениям (2.71), (2.72), (2.74) соответственно, 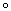 ,
,  ,
,  — расчет на базе формул (2.68), (2.69), (2.70) соответственно
— расчет на базе формул (2.68), (2.69), (2.70) соответственно
Аналогичные результаты имеют место для титановых и алюминиевых сплавов.
Обращает на себя внимание весьма сильная зависимость значений коэффициента  , получаемых расчетным путем, от вида выбранного уравнения диаграммы предельных амплитуд цикла напряжений. Причем, при использовании уравнений Гудмана и Гербера отношение расчетных значений
, получаемых расчетным путем, от вида выбранного уравнения диаграммы предельных амплитуд цикла напряжений. Причем, при использовании уравнений Гудмана и Гербера отношение расчетных значений  , получаемых по формулам (2.71) и (2.72), достигает 2,5...3 раз для сталей и титановых сплавов и 3...3,5 раз для алюминиевых сплавов.
, получаемых по формулам (2.71) и (2.72), достигает 2,5...3 раз для сталей и титановых сплавов и 3...3,5 раз для алюминиевых сплавов.
Таким образом, точность теоретической оценки коэффициента чувствительности к асимметрии цикла нагружения зависит от степени обоснованности соответствующего уравнения для диаграммы предельных амплитуд. Следует заметить, что уравнения (1.8), (1.9), (1.11), (1.12) не имеют строгого теоретического обоснования, а были получены путем анализа граничных условий и чисто умозрительных построений.
Известное уравнение И. А. Одинга
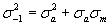 (1.10)
(1.10)
приводит к значению  = 0,41 для всех групп конструкционных металлических материалов, что также не согласуется с опытными данными.
= 0,41 для всех групп конструкционных металлических материалов, что также не согласуется с опытными данными.
Ранее было дано обоснование уравнения диаграммы предельных амплитуд цикла напряжений в виде
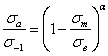 (2.58)
(2.58)
или с учетом (2.3)
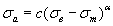 (2.59)
(2.59)
Значения параметров этих уравнений приведены в таблице 2.3.
Использование формул (2.3), (2.58) и (2.59) для теоретического определения коэффициента чувствительности к асимметрии цикла нагружения приводит к уравнениям, решение которого возможно методом последовательных приближений,
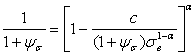 , (2.75)
, (2.75)
где c и  — параметры материала, представленные в табл. 2.3.
— параметры материала, представленные в табл. 2.3.
На рис. 2.12 показана зависимость теоретической оценки коэффициента чувствительности  (2.75) от статической прочности исследуемых материалов. Представленные графики указывают на возможность в первом приближении их аппроксимации прямыми линиями, что значительно упрощает теоретический расчет величины
(2.75) от статической прочности исследуемых материалов. Представленные графики указывают на возможность в первом приближении их аппроксимации прямыми линиями, что значительно упрощает теоретический расчет величины  , который проводится соответственно для сталей, титановых и алюминиевых сплавов по формулам
, который проводится соответственно для сталей, титановых и алюминиевых сплавов по формулам
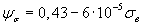 , (2.76)
, (2.76)
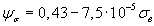 , (2.77)
, (2.77)
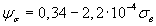 , (2.78)
, (2.78)
где 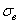 - предел прочности в МПа.
- предел прочности в МПа.
Рис. 2.12. Значения коэффициента  при различной статической прочности конструкционных материалов: 1,2,3 – соответственно для сталей, титановых и алюминиевых сплавов; сплошные линии – расчетные данные по уравнению (2.75); штриховые – аппроксимация по формулам (2.76)...(2.78).
при различной статической прочности конструкционных материалов: 1,2,3 – соответственно для сталей, титановых и алюминиевых сплавов; сплошные линии – расчетные данные по уравнению (2.75); штриховые – аппроксимация по формулам (2.76)...(2.78).
Указанная линейная аппроксимация приводит к максимальной ошибке оценки  до 5%.
до 5%.
Большую точность обеспечивает аппроксимация полином 2-ой степени
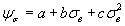 , (2.79)
, (2.79)
параметры которого представлены в табл. 2.6, где приведена также максимальная ошибка  оценки
оценки  .
.
Таблица 2.6. Значения параметров уравнения (2.79) и максимальной ошибки 
| Материал | a | b | c |  , % , %
|
| Стали | 0.5085 | -2.03·10-4 | 5.4375·10-8 | |
| Титановые сплавы | 0.4676 | -1,871·10-4 | 5.7685·10-8 | |
| Алюминиевые сплавы | 0.4032 | -5,4783·10-4 | 3.6833·10-7 |
Таким образом, из теоретического анализа следует, что с увеличением статической прочности конструкционного материала внутри одной группы коэффициент  уменьшается. Причем эта закономерность проявляется в теоретических расчетах при использовании любого из известных уравнений диаграммы предельных амплитуд и линии регрессии между пределом выносливости и статической прочностью. Поэтому ограниченные по объему экспериментальные данные, опубликованы в книге [16], говорящие о росте величины
уменьшается. Причем эта закономерность проявляется в теоретических расчетах при использовании любого из известных уравнений диаграммы предельных амплитуд и линии регрессии между пределом выносливости и статической прочностью. Поэтому ограниченные по объему экспериментальные данные, опубликованы в книге [16], говорящие о росте величины  с увеличением σв, следует считать заблуждением, объясняющимся указанным выше разбросом этой характеристики при применении ныне действующей методики усталостных испытаний.
с увеличением σв, следует считать заблуждением, объясняющимся указанным выше разбросом этой характеристики при применении ныне действующей методики усталостных испытаний.
Как показывает анализ уравнений (2.71)...(2.75), увеличение расчетного значения  с ростом статической прочности материалов возможно только в том случае, если отношение
с ростом статической прочности материалов возможно только в том случае, если отношение 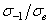 будет увеличиваться с повышением статической прочности материалов, что противоречит опытным данным и уравнениям (2.2), (2.3) и (2.12). Если принять, как это было сделано Р. Хейвудом [3], постоянное отношение для всех марок сталей
будет увеличиваться с повышением статической прочности материалов, что противоречит опытным данным и уравнениям (2.2), (2.3) и (2.12). Если принять, как это было сделано Р. Хейвудом [3], постоянное отношение для всех марок сталей 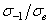 = 0.5, то расчетные значения
= 0.5, то расчетные значения  окажутся также постоянными.
окажутся также постоянными.
В частности, для всех марок сталей уравнение Р. Хейвуда [3] приводит к одинаковому значению  = 0.26.
= 0.26.
Как уже отмечалось, коэффициент чувствительности материала к асимметрии цикла оценивается на основании пределов выносливости при симметричном и отнулевом циклах напряжений. Однако, в расчетах на прочность и при схематизации циклов нагружения этот коэффициент используется и для других уровней асимметрии цикла напряжений. Более правильно, в этом случаи следует использовать изменяющийся коэффициент чувствительности к асимметрии нагружения, который можно представить в виде
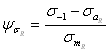 (2.80)
(2.80)
где 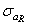 и
и 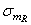 - предельные амплитуда и среднее напряжение цикла для заданного коэффициента асимметрии
- предельные амплитуда и среднее напряжение цикла для заданного коэффициента асимметрии 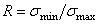 .
.
С учетом уравнения диаграммы предельных амплитуд (2.58) значение  подсчитывается методом последовательных приближений по формуле
подсчитывается методом последовательных приближений по формуле
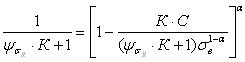 , (2.81)
, (2.81)
где
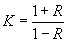
Как показывали расчеты (рис. 2.13), наибольшее отклонение от  имеет
имеет 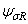 у алюминиевых сплавов так при R = 0.7...0.9 отношение
у алюминиевых сплавов так при R = 0.7...0.9 отношение 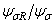 составляет 1.15...1.35.
составляет 1.15...1.35.
Причем, величина этого отношения практически не зависит от предела прочности сплавов. Для значений R = - 1.2...- 0.5 отношение указанных коэффициентов у алюминиевых и титановых сплавов, а также сталей составляет 0.93...0.97.
Максимальное значение 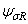 соответствует R = 1 и может быть подсчитано по формуле
соответствует R = 1 и может быть подсчитано по формуле
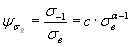
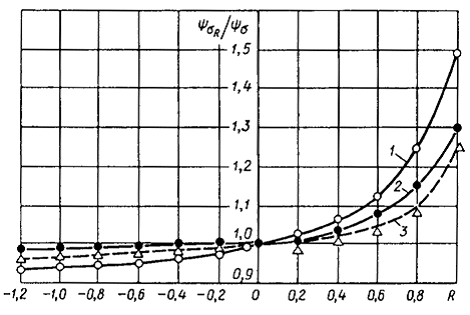
Рис. 2.13. Зависимости коэффициента 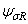 от степени асимметрии цикла напряжений: 1, 2, 3 – расчетные данные по уравнению (2.81) соответственно для алюминиевых, титановых сплавов и сталей
от степени асимметрии цикла напряжений: 1, 2, 3 – расчетные данные по уравнению (2.81) соответственно для алюминиевых, титановых сплавов и сталей
Таким образом, теоретический анализ и экспериментальные данные показывают на снижение величины коэффициента чувствительности к асимметрии цикла напряжений с ростом статической прочности материала. В связи с этим, оказываются неприемлемыми рекомендации стандарта [14] и других источников [8, 16] по методике оценки коэффициента  .
.
Теоретически обосновано и экспериментально подтверждено уравнение диаграммы предельных амплитуд (2.58) для металлических конструкционных материалов. Ранее известные и широко используемые на практике уравнения диаграммы (1.8), (1.9), (1.11) и (1.12) находятся в противоречии с опытными данными.
Дата добавления: 2015-08-08; просмотров: 849;
