Законы Стефана — Больцмана и смешения Вина

Из закона Кирхгофа (см. (198.1)) следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

Австрийский физик Й. Стефан (1835 — 1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости R_е от температуры. Согласно закону Стефана — Больцмана,

R_e = σ·T ⁴, (199.1)

т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; σ — постоянная Стефана – Больцмана: ее экспериментальное значение равно 5,67·10 ^–8 Вт/(м²·К⁴).

Закон Стефана — Больцмана, определяя зависимость R_e от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции r_λT 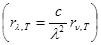от длины волны λ при различных температурах (рис. 41) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_λT от λ и осью абсцисс, пропорциональна энергетической светимости R_e черного тела и, следовательно, по закону Стефана — Больцмана, четвертой степени температуры.

Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны λ _mах, соответствующей

максимуму функции r_λT , от температуры Т. Согласно закону смещения Вина,

λ_max = b/T, (199.2)

т. е. длина волны λ _mах, соответствующая максимальному значению спектральной плотности энергетической светимости r_λT черного тела, обратно пропорциональна его термодинамической температуре, b — постоянная Вина: ее экспериментальное значение равно 2,9·10 ^-3 м · К. Выражение (199.2) потому называют законом смещения Вина, что оно показывает смещение положения максимума функции r_λT по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

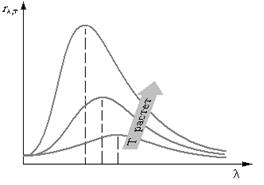
Рис. 41

Несмотря на то, что законы Стефана — Больцмана и Вина играют в теории теплового излучения важную роль, они являются частными законами, так как не дают общей картины распределения энергии по частотам при различных температурах.

Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа r_ν,T. не дал желаемых результатов.

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе,атомные осцилляторы излучают энергию не непрерывно, а определенными порциями -— квантами, причем энергия кванта пропорциональна частоте колебания :

ε ₀ = hν = hc / λ, (200.2)

где h = 6,625.10 ^-34 Дж·с — постоянная Планка.Так как излучение испускается порциями, то энергия осциллятора может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии ε ₀ :

ε = nhν (n = 0, 1, 2,…).

В данном случае среднюю энергию áeñ осциллятора нельзя принимать равной kT. Вероятность, что осциллятор находится в состоянии с энергией ε _n, пропорциональна 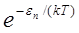, но при вычислении средних значений (при дискретных значениях энергии) интегралы заменяются суммами. При данном условии средняя энергия осциллятора

,

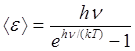а спектральная плотность энергетической светимости черного тела

.

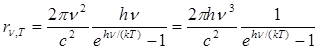Таким образом, Планк вывел для универсальной функции Кирхгофа формулу(200.3)

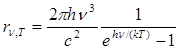, (200.3)

которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900г. на заседании Немецкого физического общест­ва. Этот день стал датой рождения квантовой физики.

Из формулы Планка, зная универсальные постоянные h, k,и с,можно вычислить постоянные Стефана — Больцмана s и Вина b . С другой стороны, зная экспериментальные значения s и b,можно вычислить значения h и k (именно так и было впервые найдено числовое значение постоянной Планка).

Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.

Законы теплового излучения используются для измерения температуры раскаленных и самосветящихся тел (например, звезд). Методы измерения высоких температур, использующие зависимость спектральной плотности энергетической светимости или интегральной энергетической светимости тел от температуры, называются оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел, различают радиационную, цветовую и яркостную температуры.

1. Радиационная температура— это такая температура черного тела, при которой его энергетическая светимость R_e (см. (198.3)) равна энергетической светимости R_T (см. (197.2)) исследуемого тела. В данном случае регистрируется энергетическая светимость исследуемого тела и по закону Стефана — Больцмана (199.1) вычисляется его радиационная температура:

.

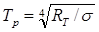Радиационная температура Т_р тела всегда меньше его истинной температуры Т.

2. Цветовая температура.Из закона Вина (см. (199.2)), зная длину волны l_mах, соответствующую максимальной спектральной плотности энергетической светимости R_lT исследуемого тела, можно определить его температуру

T_ц = b / l_mах,

которая называется цветовой температурой. Для серых тел цветовая температура совпадает с истинной. Для тел, которые сильно отличаются от серых (например, обладающих селективным поглощением), понятие цветовой температуры теряет смысл. Таким способом определяется температура на поверхности Солнца (Т_ц » 6500 К) и звезд.

3. Яркостнаятемпература Т_я – это температура черного тела, при которой для определенной длины волны его спектральная плотность энергетической светимости равна спектральной плотности энергетической светимости исследуемого тела, т. е.

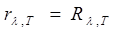, (201.1)

где Т – истинная температура тела. По закону Кирхгофа (см. (198.1)), для исследуемого тела при длине волны l,

R_l,T / A_l,T = r_l,T или учитывая (201.1) 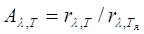. (201.2)

Т_я < Т, т.е. истинная температура тела всегда выше яркостной. При известных А_l,Т и l можно определить истинную температуру исследуемого тела.

4. Тепловые источники света.Свечение раскаленных тел используется для создания источников света, первые из которых — лампы накаливания и дуговые лампы — были соотвественно изобретены русскими учеными А. Н. Лодыгиным в 1873 г. и П. Н. Яблочковым в 1876 г.

На первый взгляд кажется, что черные тела должны быть наилучшими тепловыми источниками света, так как их спектральная плотность энергетической светимости для любой длины волны больше спектральной плотности энергетической светимости нечерных тел, взятых при одинаковой температуре. Однако оказывается, что для некоторых тел (например, вольфрама), обладающих селективностью теплового излучения, доля энергии, приходящаяся на излучение в видимой области спектра, значительно больше, чем для черного тела, нагретого до той же температуры. Поэтому вольфрам, обладая еще и высокой температурой плавления, является наилучшим материалом для изготовления нитей ламп.