Зависимость проницаемости от пористости. Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношений уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объемную скорость течения жидкости через такую пористую среду:

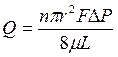, (1.22)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

μ – вязкость жидкости;

∆P- перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

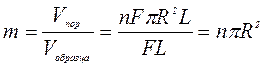, (1.23)

Следовательно, уравнение (1.22) можно переписать следующим образом:

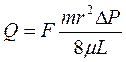,(1.24)

Из уравнения Дарси следует, что:

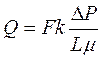, (1.25)

Приравнивая правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:

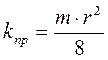, (1.26)

Из чего следует, что размер порового канала будет равен:

, (1.27)

Если выразить проницаемость в 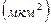, то радиус поровых каналов (в мкм) будет равен:

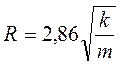, (1.28)

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнения Букингема:

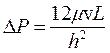, (1.29)

где h – высота трещины;

v – линейная скорость.

Подставив это выражение в уравнение Дарси, получим:

, (1.30)

Соотношение (1.25) и (1.26) справедливы только для идеальной пористой среды (например, кварцевый песок).

Для реальных условий используется эмпирическое уравнение Котяхова:

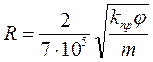(1.31)

где R – радиус пор;

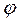– структурный коэффициент, описывающий извилистость порового пространства.

Значение 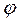можно оценить путем измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, 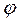изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

, (1.32)