Примеры организации циклов

Пример 2.1. Печать таблицы значений функции

Написать программу печати таблицы значений функции 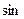для аргумента, изменяющегося в заданных пределах с заданным шагом.

Исходными данными являются начальное значение аргумента 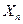конечное значение аргумента 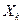и шаг изменения аргумента 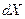. Все величины — вещественные и могут принимать любые значения на числовой оси. Результатом работы программы должна быть таблица, состоящая из двух столбцов — значений аргумента и соответствующих им значений функции. Вид таблицы приведен на рис. 2.2.

------------------------------------------

│ X │ Y │

-------------------------------------------

│ -4.00 │ 0.76 │

│ -3.00 │ -0.14 │

│ -2.00 │ -0.91 │

│ -1.00 │ -0.84 │

│ -0.00 │ -0.00 │

│ -1.00 │ -0.84 │

│ -2.00 │ -0.91 │

│ -3.00 │ -0.14 │

│ -4.00 │ -0.76 │

-------------------------------------------

Рис. 2.2. Результаты выполнения программы для ; ; .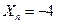

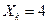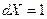1. Опишем алгоритм в словесной форме.

2. Ввести исходные данные: , , .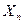

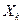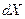3. Вывести заголовок таблицы.

4. Принять 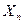в качестве первого значения аргумента.

5. Вычислить значение функции.

6. Вывести строку таблицы (текущее значение аргумента и соответствующее ему значение функции).

7. Перейти к следующему значению аргумента.

8. Если оно не превышает конечное значение, повторить шаги 4-6, иначе закончить.

Шаги 4-6 повторяются многократно, поэтому для их выполнения надо организовать цикл. На каждом проходе цикла требуется хранить одно значение аргумента и одно значение функции, поэтому для них достаточно завести по одной переменной вещественного типа. Назовем эти переменные х и у. Переменная х будет содержать текущее значение аргумента, а у — соответствующее ему значение функции:

program tabl_fun;

var

Xn, Xk : real; {начальное и конечное значения аргумента}

dX : real; {шаг изменения аргумента}

x,y: real; {текущие значения аргумента и функции}

begin

writeln ('Введите Xn, Xk, dX'); {приглашение ко вводу данных}

readln (Xn, Xk, dX); {ввод исходных данных - 1}

writeln ('------------------------------------'); {заголовок таблицы - 2}

writeln ('| X | Y |');

writeln ('------------------------------------');

x := Xn; {первое значение аргумента = Xn - 3}

while x <= Xk do begin {заголовок цикла - 7}

y := sin(x); {вычисление значение функции - 4}

writeln ('|', x:9:2, ' | ', y:9:2, ' | '); {вывод строки табл. - 5}

x :=x + dX; {переход к следующему значению аргумента - 6}

end;

writeln ('------------------------------------');

end.

Цифры в комментариях соответствуют шагам алгоритма. Обратите внимание на то, что условие продолжения цикла записано в его заголовке и проверяется до входа в цикл. Таким образом, если задать конечное значение аргумента, меньшее начального, даже при отрицательном шаге цикл не будет выполнен ни разу.

Параметром этого цикла, то есть переменной, управляющей его выполнением, является х. Для правильной работы цикла необходимо присвоить параметру начальное значение до входа в цикл, поэтому блок начальных установок цикла присутствует в явном виде (шаг 3). Начинающие часто забывают про этот блок. В данном случае при отсутствии этого оператора переменной х будет присвоено значение 0, поскольку в Паскале глобальные переменные обнуляются автоматически.

Блок модификации параметра цикла представлен оператором, выполняющимся на шаге 6. Для перехода к следующему значению аргумента текущее значение наращивается на величину шага и заносится в ту же переменную. Начинающие часто забывают про модификацию параметра, в результате чего программа «зацикливается». Если с вами произошла такая неприятность, попробуйте для завершения программы нажать клавиши Ctrl+Break, а впредь перед запуском программы для параметра цикла проверяйте:

§ присвоено ли ему начальное значение;

§ изменяется ли он на каждой итерации цикла;

верно ли записано условие продолжения цикла.

Пример 2.2. Нахождение корня нелинейного уравнения

Найти корень уравнения 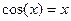методом деления пополам с точностью 0,0001.

Исходные данные для этой задачи — точность, результат — число, представляющее собой корень уравнения. Оба значения имеют вещественный тип.

Суть метода деления пополам очень проста. Задается интервал, в котором есть ровно один корень (следовательно, на концах этого интервала функция имеет значения разных знаков, как показано рис. 2.3). Вычисляется значение функции в середине этого интервала. Если оно того же знака, что и значение на левом конце интервала, значит, корень находится в правой половине интервала, иначе — в левой. Процесс повторяется для найденной половины интервала до тех пор, пока его длина не станет меньше заданной точности.

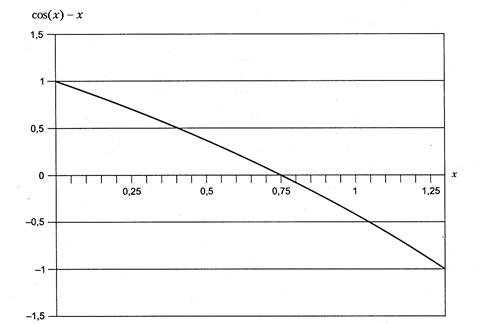
Рис. 2.3. График функции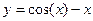

В приведенной далее программе исходный интервал задан с помощью констант, значения которых взяты из графика функции. Для уравнений, имеющих несколько корней, можно написать дополнительную программу, определяющую интервалы, содержащие ровно один корень, путем вычисления и анализа таблицы значений функции:

program root;

var x, L, R : real;

begin

L := 0; R := 1; {левая и правая границы интервала}

repeat

x := (L + R) / 2; {середина интервала}

if (cos(x) - x) * (cos(L) - L)<0 {если значения разных знаков, то}

then R := x {корень в правой половине интервала}

else L := x {иначе корень в левой половине интервала}

until abs(R - L) < 1e-4;

writeln('Корень равен', x:9:4);

end.

Пример 2.3. Пифагоровы числа

Написать программу, которая выводит на печать все пифагоровы числа, не превышающие 15.

Пифагоровы числа — это тройки натуральных чисел, таких, что треугольник, длины сторон которого пропорциональны (или равны) этим числам, является прямоугольным.

Будем решать эту задачу методом перебора вариантов. Возведя в квадрат каждую пару натуральных чисел в заданных пределах, проверим, не является ли их сумма квадратом натурального числа:

program Pyfagor;

const

n = 15;

var

a, b, c, cx : integer;

begin

for a := 1 to n do

for b := a to n do begin { перебор всех пар чисел от 1 до 15 }

cx := sqr(a) + sqr(b); { сумма квадратов пары чисел }

c := trunc(sqrt(cx)); { кандидат на третье число }

if (sqr(c) = cx) and (c <= n) then writeln (a:3, b:3, c:3);

end;

end.

Задание.

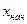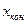Вычислить и вывести на экран в виде таблицы значения функции, заданной графически (см. задание 1 предыдущего занятия), на интервале от до с шагом 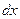. Интервал и шаг задать таким образом, чтобы проверить все ветви программы. Таблицу снабдить заголовком и шапкой.

program tabl_fun;

var

Xn, Xk : real;

dx : real;

x,y : real;

begin

writeln('введите Xn, Xk, dx');

readln ( Xn, Xk, dx);

writeln ('-----------------------------');

writeln('| X ! Y |');

writeln ('-----------------------------');

x:=Xn;

while x<=Xk do begin

if x >= -3 then y := -2 * x - 5;

if (x>=-2) and ( x<0 ) then y:=-sqrt(1-sqr(x + 1)) - 1;

if (x>=0) and (x<1) then y:=x-1;

if x>=1 then y:= sqrt(1-sqr(x-2));

writeln ('|', x:9:2,' |', y:9:2, ' |');

x:=x+dX;

end;

writeln ('-----------------------------');

end.