Добавить
Нажмите на кнопку, чтобы, не возвращаясь в окно диалога Параметры поиска решения, наложить новое условие на поиск решения задачи.
На примере рассмотрим, как с помощью средства поиска решений решаются линейные оптимизационные задачи.
Требуется определить, в каком количестве надо выпустить продукцию четырех типов: П1, П2, П3, П4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурсов каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 1.
Таблица 1
| Ресурс | П1 | П2 | П3 | П4 | Знак | Наличие |
| Прибыль | max | |||||
| Трудовые | £ | |||||
| Сырье | £ | |||||
| Финансы | £ |
Составим математическую модель, для чего введем следующие обозначения:
xj – количество выпускаемой продукции j- типа, j=1..4;
bi – количество распределяемого ресурса i- го вида, j=1..3;
aij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа;
cj – прибыль, получаемая от реализации единицы продукции j- го типа.
Математическая модель задачи будет иметь вид:
Z=60x1+70x2+120x3+130x4®max
x1+x2+x3+x4£16
6x1+5x2+4x3+3x4£110
4x1+6x2+10x3+13x4£100
xj³0; j=1..4
где х1,х2,х3,х4 – количество выпускаемой Прод1, Прод2, Прод3, Прод4.
Для решения этой задачи в EXCEL с помощью средства «Поиска решений» введем данные как показано на рис.1.
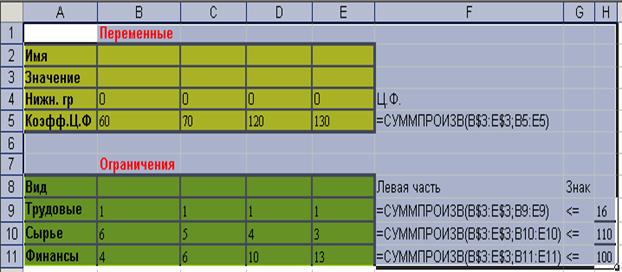
Рис.1
В ячейку F5 ввести целевую функцию. В ячейки F9:F11 ввести левые части ограничений по ресурсам (трудовым, сырью, финансам). Для этого скопировать формулу F5 в ячейки F9:F11.
Теперь выберем командуСервис, Поиск решения и заполним открывшееся диалоговое окноПоиск решения :
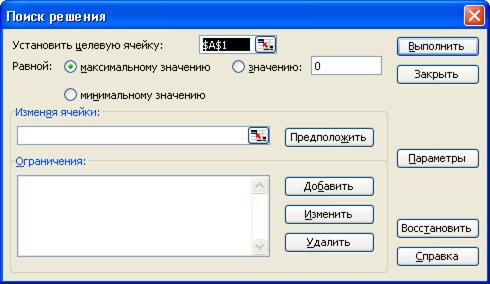
Установить целевую функцию F5;
В поле Равной - Максимальное значение;
В поле Изменяя ячейки - B3:E3;
В поле Ограничения
F9<=H9;
F10<=H10;
F11<=H11;
B3>=B4;
C3>=С4;
D3>=D4;
E3>=E4;(Для ввода ограничений использовать кнопку Добавитьдиалогового окна Поиск решения.
Необходимо в диалоговом окнеПараметры поиска решения
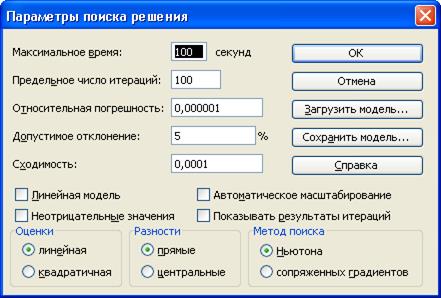
установить флажок Линейная модель. После нажатия кнопкиВыполнить получим оптимальное решение задачи.
Результаты решения представлены на рис.2
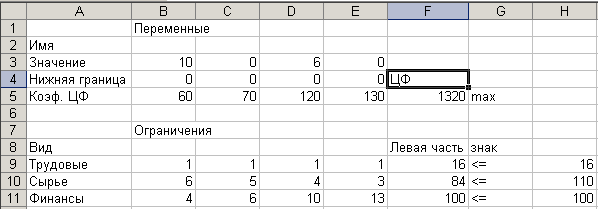
Дата добавления: 2015-08-08; просмотров: 847;
