Непараметрические критерии оценки вероятности результатов исследований
Рассмотренные в предыдущих разделах статистические параметры (среднее арифметическое, среднее квадратичное отклонение, коэффициент вариации, средняя ошибка), используются для анализа вариационных рядов, являются его параметрами и требуют представления выходных данных в количественном виде. Однако при проведении медицинских исследований достаточно часто приходится использовать методы статистического анализа данных, представленных в полуколичественном, полу качественном и качественном виде. Совокупность статистических методов, что позволяют оценить их результаты как в количественном (численном), так и в полуколичественном и качественном виде объединяют в группу непараметрических критериев оценки. Использование их не потребует расчета параметров вариационного ряда. Тут имеет значение порядок расположения вариантов в совокупностях. Статистическая оценка наблюдений с помощью непараметрических критериев, как правило, проще, нежели оценка параметрическими методами и не требует громоздких расчетов.
Преобладающая большинство параметрических статистических методик предусматривает наглядность нормального распределения вариантов в исследуемой совокупности. Однако на практике встречается не только нормальное распределение, но и другие распределения признаков. Наглядность таких ситуаций использования параметрических критериев повышает достоверность ошибок. Практическое использование непараметрических критериев, не связано с определенной формой распределения исследуемых признаков, делает целесообразным их самостоятельное использование или в комплексе с непараметрическими критериями.
Не взирая не определенную простоту методик, надежность непараметрических критериев достаточно высока. Они могут быть использованы для оценки вероятности медико-биологических результатов одной совокупности, разницы двух и более выборочных совокупностей.
Учитывая, что одним из наиболее важных разделов их использования является оценка вероятности разницы сравниваемых наблюдений, весь комплекс указанных методик можно разделить на две группы:
· Непараметрические критерии оценки вероятности разницы в двух взаимосвязанных совокупностях;
· Непараметрические критерии оценки вероятности разницы в двух независимых совокупностях.
Первую группу используют для оценки вероятности разницы по результатам, которые получены для одной группы больных на протяжении разных периодов (до лечения - после лечения, первый день - пятый день и др.). Сравнение их результатов может быть проведено по критериям знаков и Вилкоксона.
Критерий знаков - позволяет включить в анализ до 100 пар наблюдений и базируется на подсчете числа однонаправленных результатов при парном их сравнении.
В табл.1 приведена динамика скорости оседания эритроцитов (СОЭ) за 10-дневный период лечения.
Таблица 1
Динамика скорости оседания эритроцитов (СОЭ)
| Больные (№ п\п) | СОЭ | Направленность разницы | |
| 1 день | 10 дней | ||
| + | |||
| - | |||
| + | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| + | |||
| = |
Основные этапы расчета по критериям знаков:
1. Определения направленности разницы в сравниваемых группах результатов. Динамика при том отмечается соответствующими знаками: +, -, =. В дальнейшем расчете включают результаты без динамики (=).
2. Подсчет числа наблюдений с позитивными и негативными результатами. Из 10 приведенных изменения выявились у 9 больных.
3. Подсчет числа знаков, которые реже встречаются. Снижение СОЭ (-) выявлено у 6 больных, а прирост (+) зарегистрирован в трех случаях.
4. Сравнение меньшего числа знаков ( критерий Z ) с табличными критическими значениями для соответствующего числа наблюдений. Для n=9 определенный критерий Z=3 выше граничного табличного (Z0,05 =2), Поэтому нельзя сделать вывод про существенность динами скорости оседания эритроцитов - достоверность ошибки больше 5% (р > 0,05),
T-критерий Вилкоксона предусматривает возможность по-парного сравнения от 6 до 25 пар наблюдений. Его целесообразно использовать в тех случаях, когда выявляется неоднозначные количественные изменения исследуемого параметра (снижение и повышение). При этом учитывают не только направление разницы, но и ее величину.
Методика анализа по Т-критерию Вилкоксона приведена в табл. 2.
Таблица 2
Уровень артериального давления при гипертонической болезни до и после лечения
| Больные | Уровень артериального давления | Разница | Ранг разницы | Сумма рангов "+" | Сумма рангов "-" | |
| До лечения | После лечения | |||||
| В. | -35 | 6,5 | 6,5 | - | ||
| Д. | - | - | - | |||
| К. | -35 | 6,5 | 6,5 | - | ||
| Р. | +25 | - | ||||
| Н. | -30 | - | ||||
| Р. | -40 | - | ||||
| А. | +5 | - | ||||
| С. | -20 | - | ||||
| Ю. | -45 | - | ||||
| Т. | -15 | - | ||||
| T=40 | T=5 |
1. Определяется разница в парах наблюдения между верхним и нижним уровнями артериального давления.
2. Рангование полученных результатов по величине разницы между показателями без учета направленности изменений. Результаты без динамики исключают из дальнейшей оценки. Если два результата имеют одинаковые абсолютные значения изменений, то их ранги обозначают как полу сумму порядковых номеров.
3. Подсчет суммы однозначных рангов (положительных и отрицательных ).
4. Оценка по меньшей сумме рангов происходит путем сравнения определенного t-критерием с табличным значением при соответствующим числе пар наблюдений.
Критерий Вилкоксона Т=5 не превышает табличного значения для данного числа наблюдений n= 9, T0,05 =6. Однако можно сделать вывод о сущности (статистической вероятности) динамики артериального давления у больных после лечения.
Другая группа непараметрических критериев - критерии, которые используют в случае сравнения независимых совокупностей. Такими типовыми примерами их практического использования является сравнение исследуемой и контрольной групп больных, результатом двух групп наблюдений, что относится к различным заболеваниям или степени тяжести патологии. Для сравнения независимых совокупностей используют:
· Серийный критерий;
· Критерий Уайта;
· Критерий Ван дер Вардена.
Однако наиболее мощным в данной группе является критерий Колмогорова-Смирнова ( λ2 ), методика использования его приведена ниже в таблице 3.
Таблице 3
Изменение радиоактивности крови облученных животных, которые получали (Х) лечение и не получали (У) лечение(условные единицы)
| Варианты по ряду Х и У | Частоты вариантов по группам | Накопленные частоты по группам | Накопленные части по группам | Разница │(Sx / nx)- -(Sy / ny )│ | |||
| Px | Py | Sx | Sigh | Sx / nx | Sy / ny | ||
| 0,23 | 0,23 | ||||||
| 0,56 | 0,56 | ||||||
| 0,67 | 0,23 | 0,44 | |||||
| 0,78 | 0,34 | 0,44 | |||||
| 0,89 | 0,34 | 0,55 | |||||
| 0,45 | 0,55 | ||||||
| 0,56 | 0,44 | ||||||
| 0,67 | 0,33 | ||||||
| 0,89 | 0,11 | ||||||
| Nx=9 | Ny=8 |
1. Числовые значения двух вариационных рядов объединяют в один вариационный ряд, варианты которого размещают в порядке возрастания.
2. Определяют частоты вариантов для обеих групп наблюдений.
3. Определяют полученные частоты для обеих групп.
4. Определяют полученные части , для чего накопленные частоты делятся на число наблюдений для каждой группы.
5. Рассчитывается разница полученных частот групп Х и У без учета знаков.
6. Определяют максимальную разницу - Д=0,55 (графа 8, таблица 3).
7. Определяют критерий ( λ2 ) по формуле
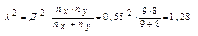
8. Cравниваем полученный результат с предельным значениями критерия Колмогорова-Смирнова. Если λ2 больше предельного значения, то разница между сравниваемыми группами является существенной.
Для данного задания λ2 =1,28. Сравнивая полученный результат с пограничным значением λ20,05 =1,84 и λ20,01=2,65, делаем вывод о не существенность разницы между сравниваемыми группами.
Дата добавления: 2015-08-04; просмотров: 856;
