Давление в покоящейся жидкости


Давлением в покоящейся жидкости называется напряжение сжатия (рис.1-1)

 ,
, 
 (І-1)
(І-1)
где  - давление в точке А;
- давление в точке А;  - элементарная площадка, содержащая точку А;
- элементарная площадка, содержащая точку А; 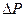 - сжимающая сила, действующая на площадку
- сжимающая сила, действующая на площадку  .
.
Давление направлено по нормали к площадке, его величина не зависит от ориентировки площадки в пространстве и является функцией координат точек жидкости:
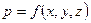 , (І-2)
, (І-2)
В международной системе единиц физических величин единицей измерения давления является 1H/м2 - паскаль (Па). Более удобными для практического использования являются кратные единицы - килопаскаль (кПа) и мегапаскаль (МПа):
1 кПа = 103 Па; 1 МПа = 106 Па.
Давление, представляющее полное напряжение сжатия от действия всех внешних сил (поверхностных и массовых), приложенных к жидкости, называется абсолютным давлением.
В технике удобно отсчитывать давление от условного нуля, за который принимается давление атмосферного воздуха на поверхности земли, равное примерно 100кПа. Если величина давления показывает избыток абсолютного давления p над атмосферным pа, то называется манометрическим (избыточным) давлением p:
ри = р - pат. (І-3)
Избыточное давление отрицательно, если абсолютное давление меньше атмосферного. Недостаток давления до атмосферного называется вакуумом  pв;
pв;
рв= pат - p. (І-4)
или
pв = - p. (І-5)
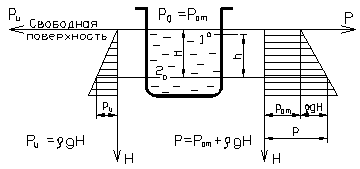
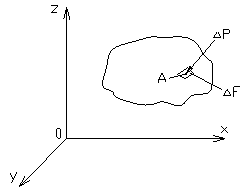

Рис. І - 1 Рис. І - 2
В однородной несжимаемой жидкости, покоящейся под действием силы тяжести (рис. І - 2), давление нарастает с глубиной по закону
p2 = p1 + 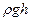 , (І-6)
, (І-6)
Где p1 - давление в произвольной точке 1 жидкости; p2 - давление в точке 2 на глубине h, отсчитанной от уровня точки 1; 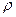 - плотность жидкости; g - ускорение свободного падения.
- плотность жидкости; g - ускорение свободного падения.
Эта зависимость представляет основной закон равновесия жидкости в однородном поле тяжести.
Поверхностями уровня (поверхностями равного давления) в рассматриваемом случае равновесия жидкости являются горизонтальные плоскости.
При определении давления в точках жидкости, заполняющей открытый в атмосферу сосуд, удобно в качестве исходной точки 1 брать точку на свободной поверхности, где известно действующее на жидкость внешнее давление, равное атмосферному,. При этом абсолютное давление в произвольной точке жидкости
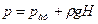 , (І-7)
, (І-7)
где H - глубина расположения точки под уровнем жидкости.
Избыточное давление, создаваемое в данном случае только весом жидкости,
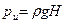 . (І-8)
. (І-8)
Так, для воды (  = 1000 кг|м3) избыточное давление на глубине H = 10м равно (при g = 9,81 м/с2) pи = 98,1 кПа.
= 1000 кг|м3) избыточное давление на глубине H = 10м равно (при g = 9,81 м/с2) pи = 98,1 кПа.
Формула (1- 8) даёт возможность выражать избыточное давление в любой точке жидкости пьезометрической высотой, т.е. величиной H заглубления данной точки под пьезометрической плоскостью атмосферного давления, проходящей через уровень в пьезометре, присоединённом к сосуду (рис. 1-3).
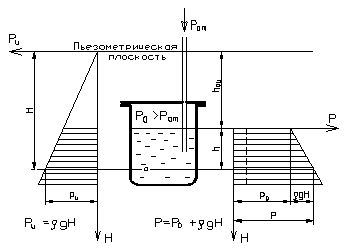
Рис. 1 - 3
Если сосуд закрыт и на поверхность жидкости действует избыточное давление (действующее на жидкость внешнее давление pо больше окружающего атмосферного давления pат), то пьезометрическая плоскость располагается над свободной поверхностью жидкости на высоте

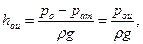 (І- 9)
(І- 9)
где pои - избыточное давление на поверхности жидкости.
Если на поверхность жидкости действует вакуум (pо< pат), то пьезометрическая плоскость находится под поверхностью жидкости на высоте
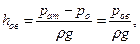 (І-10)
(І-10)
где pов - вакуум на поверхности жидкости .
Помещенные в данной главе задачи на определение давления в несжимаемой жидкости могут быть решены с помощью уравнений, выражающих:
1) условие равновесия жидкости;
2) условие равновесия твердого тела, на которое действует сила давления со стороны жидкости.
Задачи: 
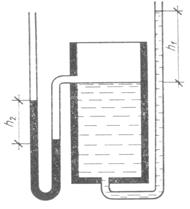
№ 1.1
Определить давление p в котле и пьезометрическую высоту 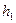 , если высота поднятия ртути в ртутном манометре , если высота поднятия ртути в ртутном манометре 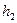 . .
| 
| ||||||||||
| Исходные данные | Номер варианта | ||||||||||
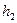 , м , м
| |||||||||||
№ 1.2
| Определить давление p в сосуде по показаниям жидкостного манометра, если слева над ртутью налито масло, а справа – вода. | 
| ||||||||||
| Исходные данные | Номер варианта | ||||||||||
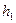 , м , м
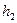 , м , м
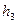 , м , м
| 1,5 0,8 0,15 | 1,0 0,3 0,10 | 1,8 0,4 0,2 | 2,0 0,6 0,12 | 1,3 0,2 0,13 | 1.7 0.5 0.18 | 1.4 0.3 0.14 | 1.9 0.7 0.16 | 1.2 0.4 0.17 | 1.1 0.2 0.11 | |
№ 1.3
Определить избыточное давление воды в трубе В, если показание манометра  . Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем известны H1, H2, H3 . Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем известны H1, H2, H3
| 
|
Как изменится показание манометра, если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран К)? Высота H3 известна.
| Исходные данные | Номер варианта | |||||||||
H1, м
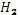 , м , м
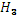 , м
PM, МПа , м
PM, МПа
| 0,5 3,0 5,0 0,025 | 1,0 4,0 6.0 0,04 | 0,6 3,2 5,3 0,03 | 0,9 3,8 5,9 0,035 | 1.1 4,2 6,3 0,045 | 0.7 3,4 5,5 0,032 | 0,4 2,8 4,5 0,023 | 0,8 3,6 5.7 0,03 | 0,3 2.5 4,0 0,020 | 1,2 4,3 6,4 0,04 |
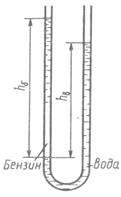
№ 1.4
В U-образную трубку налиты вода и бензин. Определить плотность бензина, если известны 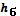 ,мм и ,мм и  ,мм. Капиллярный эффект не учитывать. ,мм. Капиллярный эффект не учитывать.
| 
|
| Исходные данные | Номер варианта | |||||||||
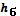 , мм , мм
 , мм , мм
|
№ 1.5
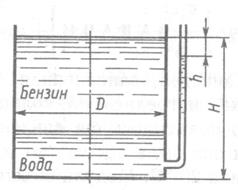
В цилиндрический бак диаметром D, м до уровня H, м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h,мм. Определить вес находящегося в баке бензина, если  . .
| 
|
| Исходные данные | Номер варианта | |||||||||
| D, м H, м h, мм | 2,0 1,5 | 1,5 1,6 | 1,0 1,7 | 0,5 2.0 | 2,5 1,4 | 1,2 1,8 | 1,8 1,9 | 3,0 2,1 | 2,2 1,5 | 2,6 1.6 |
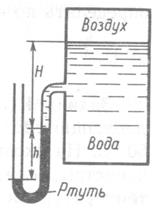
№ 1.6
Определить абсолютное давление воздуха в сосуде, если показание ртутного прибора h, мм, высота Н, м. Плотность ртути 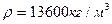 . Атмосферное давлениеPат,мм рт.ст. . Атмосферное давлениеPат,мм рт.ст.
| 
|
| Исходные данные | Номер варианта | |||||||||
| Рат, мм рт. ст. H, м h, мм | 1,4 | 1,36 | 1,3 | 1,55 | 0,95 | 1.35 | 1.45 | 1.6 | 1.65 |
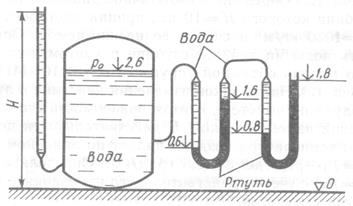
№ 1.7
Определить избыточное давление 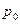 воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты 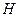 должен быть пьезометр для измерения того же давления должен быть пьезометр для измерения того же давления 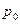 ? Плотность ртути ? Плотность ртути 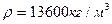 . .
|
№ 1.8
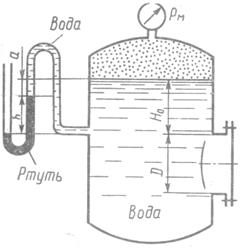
Определить силу давления жидкости (воды) на крышку люка диаметром 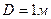 в следующих двух случаях, если известны:
1) показания манометра PM, МПа и H0,м;
2) показания ртутного вакуумметра при h, мм и а,м, в следующих двух случаях, если известны:
1) показания манометра PM, МПа и H0,м;
2) показания ртутного вакуумметра при h, мм и а,м, 
| 
|
| Исходные данные | Номер варианта | |||||||||
| PM, МПа H0, м h, мм а, м | 0,08 1,5 73.5 1.0 | 0,1 1.0 1.2 | 0,15 1.2 0,9 | 0.07 2.0 0.8 | 0,17 0,9 1,5 | 0.2 1.4 83,5 1.3 | 0.06 1.9 87.5 1.4 | 0.04 1.1 68.5 0,7 | 0.12 1.3 72.5 1.1 | 0.19 0.5 1.0 |
№ 1.9
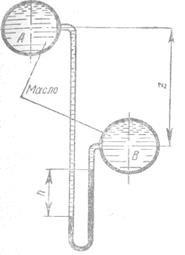
Найти разность гидростатического давления в точках А и В, расположенных на оси цилиндров. Цилиндры заполнены минеральным маслом ( 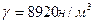 ); разность уровней в ртутном манометре ); разность уровней в ртутном манометре  ; разность осей цилиндров ; разность осей цилиндров 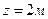 . .
| 
|
| Исходные данные | Номер варианта | |||||||||
| h, мм z,м | 2,5 | 3.5 | 1.5 | 2.2 | 2,8 | 3.0 | 3.6 | 2.1 | 2.4 |
№ 1.10
В закрытом резервуаре на поверхности жидкости поддерживается постоянное давление 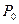 . Показания пьезометра, присоединенного к резервуару - . Показания пьезометра, присоединенного к резервуару -  . .
| 
|
Определить абсолютное и избыточное давление на поверхности жидкости, а также показания дифференциального ртутного манометра  , если уровень ртути в открытой трубке манометра расположен ниже уровня жидкости в резервуаре на величину
, если уровень ртути в открытой трубке манометра расположен ниже уровня жидкости в резервуаре на величину 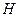 . Барометрическое давление наружного воздуха -
. Барометрическое давление наружного воздуха - 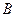 . Данные для решения взять из табл.:
. Данные для решения взять из табл.:
| Последняя цифра шифра | Жидкость |  , см , см
| 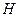 ,см ,см
| 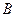 , мм рт.ст. , мм рт.ст.
|
| Вода Керосин Нефть легкая Спирт Глицерин Масло касторовое Бензин Масло трансформ. Дизтопливо Нефть тяжелая |

 1.2 Силы давления покоящейся жидкости на плоские стенки
1.2 Силы давления покоящейся жидкости на плоские стенки
Если плоская стенка подвергается одностороннему давлению жидкости (на не смоченной стороне стенки – атмосферное давление), то результирующая P сил давления, воспринимаемая стенкой и нормальная к ней (рис. І-4),
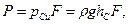 (1 – 11)
(1 – 11)
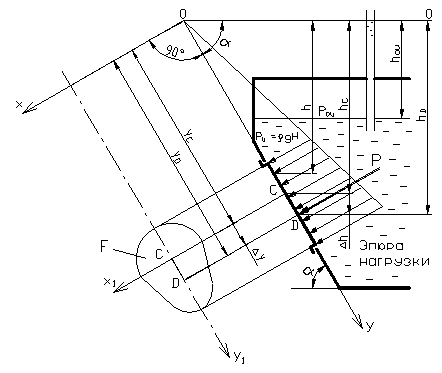
Рис. І – 4
где 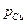 - избыточное давление в центре тяжести площади F; F - смоченная площадь стенки;
- избыточное давление в центре тяжести площади F; F - смоченная площадь стенки;  - расстояние по вертикали от центра тяжести площади F до пьезометрической плоскости 0 – 0;
- расстояние по вертикали от центра тяжести площади F до пьезометрической плоскости 0 – 0;
при избыточном давлении p0и на свободной поверхности эта плоскость проходит над свободной поверхностью жидкости на расстоянии h0и = p0и/( 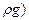 , при вакууме p0в – под свободной поверхностью на расстоянии h0в= p0в/(
, при вакууме p0в – под свободной поверхностью на расстоянии h0в= p0в/( 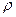 g), при вакууме p0в – под свободной поверхностью на расстоянии h0в = p0в/ (
g), при вакууме p0в – под свободной поверхностью на расстоянии h0в = p0в/ ( 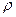 g ).
g ).
Если p0и – 0, то пьезометрическая плоскость совпадает со свободной поверхностью, и нагрузка на стенку создаётся только давлением жидкости.
Центр давления – точка пересечения линии действия силы P c плоскостью стенки. Положение центра давления (точка D на рис. І – 4) в плоскости стенки определяется формулами
 ; (І –12)
; (І –12)
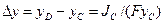 , (І –13)
, (І –13)
где yD и yC – расстояние от центра давления D и центра тяжести С площадки стенки до линии пересечения плоскости стенки с пьезометрической плоскостью (ось х на рис. І – 4); 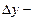 смещение центра давления относительно центра тяжести вдоль оси y; JC – момент инерции площади стенки относительно горизонтальной оси x1, проходящей через центр тяжести площади стенки.
смещение центра давления относительно центра тяжести вдоль оси y; JC – момент инерции площади стенки относительно горизонтальной оси x1, проходящей через центр тяжести площади стенки.
Задачи:
№ 2.1
| Заглушка А прижата к торцу горизонтального цилиндрического резервуара диаметром D при помощи домкрата B, установленного в ее центре. Резервуар наполовину заполнен жидкостью. | 
|
Определить:
1) Определить наименьшую силу Р нажатия домкрата. необходимую для удержания заглушки.
2) При каком вакууме V над водой в резервуаре заглушка могла бы удержаться без домкрата.
| Исходные данные | Номер варианта | |||||||||
| Жидкость D, м | вода 1,2 | керосин 1,4 | нефть легкая 1.5 | спирт 1,7 | 
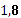
| масло касторовое 2,0 | бензин 2,2 | дизтопливо 1,9 | нефть тяжелая 2,4 | масло трансформ. 1,6 |
№ 2.2
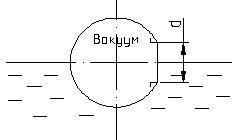
Аппарат, плавающий на поверхности воды (  ), имеет люк, закрытый изнутри плоской крышкой диаметром d.
Определить силу давления F на крышку, если внутри аппарата вакуум Рв . ), имеет люк, закрытый изнутри плоской крышкой диаметром d.
Определить силу давления F на крышку, если внутри аппарата вакуум Рв .
| 
|
Найти расстояние 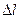 линии действия этой силы до оси люка.
линии действия этой силы до оси люка.
| Исходные данные | Номер варианта | |||||||||
d, м
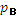 , КПа , КПа
| 0,8 3,0 | 0,5 2,0 | 1,0 4.0 | 1,2 2,5 | 0,6 3,5 | 0,9 4,5 | 1,5 1,5 | 0,7 1.0 | 1,1 0,5 | 1,4 1.8 |
№ 2.3
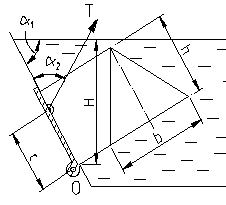
Определить минимально необходимое натяжение T каната и реакцию R0 на оси поворота О щита, закрывающего треугольное отверстие в плоской стенке, если заданы линейные размеры:
 и углы и углы 
| 
|
| Исходные данные | Номер варианта | |||||||||
Н,м
h,м
b,м
с,м
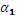 ,° ,°
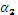 ,° ,°
| 3.2 2.0 1.6 1.8 | 3.5 2.5 1.8 2.3 | 4.3 3.6 1.9 3.4 | 4.0 3.0 2.0 2.8 | 4,8 2.8 2.5 2.6 | 5.5 3.2 2.5 2.5 | 5.2 3.2 2.6 3.0 | 6.0 4.0 2.8 3.8 | 2.8 1.9 1.5 1.7 | 4.5 3.5 2,2 3,0 |
№ 2.4
| Клапанный затвор, имеющий плоскую поверхность размером L x B м, создает подпор воды H. Определить: 1) Суммарную силу натяжения тросов Т, удерживающих затвор в заданном положении (без учета Mтр в опоре). | 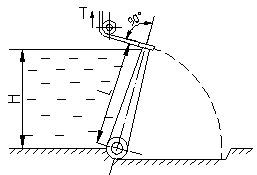
|
2) Силу R, воспринимаемую цапфами опоры.
| Исходные данные | Номер варианта | |||||||||
| Н,м L,м B,м | 2.3 2,5 | 2,7 3.0 | 3.0 3.5 | 3,4 3.9 | 3,8 4,6 | 4.3 5.0 | 4.6 5.5 | 4.9 5.8 | 5,2 6.0 | 5.5 6.1 |
№ 2.5
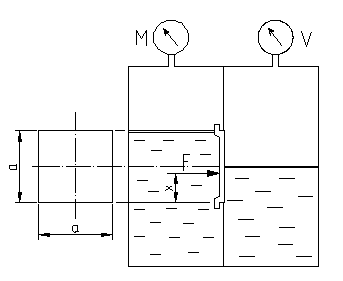
Замкнутый резервуар с нефтью ( 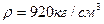 ) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной ) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной 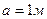 . Давление над нефтью в левой части резервуара определяется показанием манометра M, а в правой – показанием вакуумметра V. . Давление над нефтью в левой части резервуара определяется показанием манометра M, а в правой – показанием вакуумметра V.
| 
|
Уровни нефти указаны на рисунке. Найти значение и плечо x результирующей силы F давления на крышку, закрывающее отверстие в перегородке.
| Исходные данные | Номер варианта | |||||||||
| PM, КПа PV, КПа |
№ 2.6
| Отверстие в перегородке замкнутого сосуда закрыто круглой крышкой D. Левая секция заполнена ртутью до центра крышки, над ртутью находится газ под абсолютным давлением P1. В правой секции находится газ под абсолютным давлением P2. | 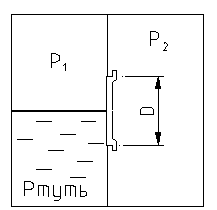
|
Определить:
1) Силу давления F на крышку при P2 =0;
2) При каком P2 сила F будет равна нулю.
| Исходные данные | Номер варианта | |||||||||
| P1, КПа D, м | 0,4 | 0,5 | 0.8 | 1,2 | 0,6 | 1,0 | 0.7 | 0.9 | 0.6 | 1.1 |
№ 2.7
| Прямоугольный поворотный щит размером L x B закрывает выпускное отверстие плотины. Справа от щита уровень воды H1, слева H2 . Определить: 1) Начальную силу T натяжения тросов, необходимую для открытия щита, если пренебречь трением в цапфах. | 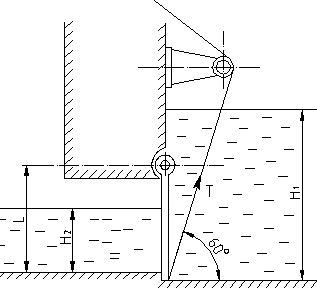
|
2) С какой силой FА щит прижимается к порогу А в закрытом положении, если принять, что по боковым сторонам щита опоры отсутствуют.
| Исходные данные | Номер варианта | |||||||||
| H1, м H2, м L, м В, м | 5.0 2.0 3.0 4.0 | 5.5 2.5 3.5 5.5 | 6.0 3.0 4.0 5.0 | 8.0 5.0 6.0 7.5 | 7.0 4.0 5.0 | 6.5 3.5 4.5 12,5 | 6.0 7.5 | 9.5 5.5 7.0 5.0 | 7.5 4.5 5.5 7.5 | 9.0 6.5 8.0 |
№ 2.8
| Сила давления воды через обшивку прямоугольного щита высотой H и шириной В передается на четыре горизонтальные балки. На каких расстояниях x от свободной поверхности следует располагать, чтобы они были нагружены одинаково? Найти силу давления F на весь щит. | 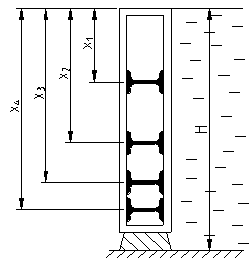
|
| Исходные данные | Номер варианта | |||||||||
| Н, м В, м | 4.0 6.0 | 6.0 7.5 | 8.0 10.0 | 5.0 7.0 | 7.0 10.5 | 9.0 12.5 | 3.0 5.0 | 7.5 10.0 | 4.5 6.5 |
№ 2.9
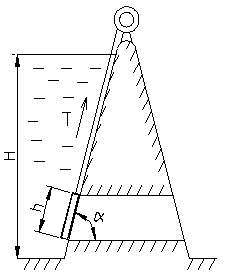
Плоский затвор, закрывающий выпускное отверстие в плотине, может перемещаться по ее стене, наклоненной к горизонту под углом 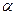 , глубина воды H.
Размеры затвора: h, b, m – масса затвора.
Определить силу Т, необходимую для начального смещения закрытого затвора вверх, если коэффициент трения скольжения затвора в направляющих f=0.3. , глубина воды H.
Размеры затвора: h, b, m – масса затвора.
Определить силу Т, необходимую для начального смещения закрытого затвора вверх, если коэффициент трения скольжения затвора в направляющих f=0.3.
| 
|
| Исходные данные | Номер варианта | |||||||||
 ,°
h, м
Н, м
b, м
m, т ,°
h, м
Н, м
b, м
m, т
| 1,8 6.0 2.4 2.0 | 2.0 5.8 2.5 2.3 | 2.2 5.6 3.0 2.5 | 2.4 5.4 3.2 2.7 | 2.6 5.2 3.5 3.0 | 1.9 5.0 3.0 2.1 | 1.7 4.8 2.3 1.9 | 1.6 4.6 2.2 1.8 | 2.1 5.9 2.7 2.4 | 2.3 5.7 2.9 2.6 |
№ 2.10
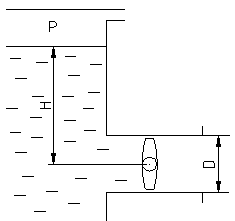
Закрытый резервуар с жидкостью (плотность  ) имеет выпускную трубу диаметром D, перекрытую дисковым затвором. Избыточное давление в резервуаре р, глубина над центром дискового затвора Н.
Найти силу давления F на клапан затвора и момент М этой силы относительно оси поворота затвора. ) имеет выпускную трубу диаметром D, перекрытую дисковым затвором. Избыточное давление в резервуаре р, глубина над центром дискового затвора Н.
Найти силу давления F на клапан затвора и момент М этой силы относительно оси поворота затвора.
| 
|
Каковы будут сила давления F / и момент М /, если P=Pат .
| Исходные данные | Номер варианта | |||||||||
| р, КПа Н, м D, м | 6.0 0.5 0.5 | 7.0 0.6 0.6 | 8.0 0.65 0.7 | 9.0 0.7 0.8 | 10.0 0.75 0.9 | 11.0 0.8 1.0 | 12.0 0.85 0.6 | 13,0 0.9 0.7 | 14.0 0.95 0.8 | 15.0 1.0 0.9 |
Дата добавления: 2015-08-01; просмотров: 3684;
