Сравнение периодов колебаний оборотного и математического маятников.

1.Задать длину математического маятника. Для этого: установить нижний кронштейн на уровне L = a₁ + a₂ = 29 см и закрепить зажимным винтом 7.

2. Установить математический маятник: а) ослабить зажимный винт 12; б) повернуть верхний кронштейн на 180 вокруг оси колонки и вновь закрепить его; в) вращая вороток 13 на верхнем кронштейне, подвести маятник к фотоэлементу так, чтобы риска на шарике была продолжением черты на корпусе нижнего кронштейна 5.

3. Определить период колебаний математического маятника:

а) привести маятник в движение, с угловой амплитудой ~4 ÷ 5^о. Выждав несколько периодов колебания, нажать на кнопку «СБРОС»;

б) после подсчета измерителем N – 1 колебаний нажать на клавишу «СТОП». При этом на индикаторах 9 и 10 зафиксируются время t и число полных колебаний N;

в) результаты измерения времени t и числа N = 10 полных колебаний записать в таблицу. Опыт повторить 2 раза, вычислить среднее время 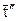и по формуле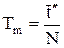

определить период колебаний математического маятника. Сравнить полученный период Т_m с периодом оборотного маятника Т и дать заключение об изохронности колебаний обоих маятников.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется физическим маятником? Математическим?

2. Запишите формулы для периодов физического и математического маятников.

3. Что такое приведенная длина физического маятника? (Написать формулу приведенной длины).

4. Что такое центр качания физического маятника? Где он находится? Чем замечательны точки подвеса и центр качания маятника?

5. Доказать, что два периода оборотного маятника с сопряженными осями равны между собой Т₁ = Т₂.

6. Почему в маятнике, используемом в работе, опорные призмы расположены асимметрично относительно точки центра тяжести?

7.