Пространственная система сил. Теорема:Если пространственная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой точки равен геометрической сумме моментов

Теорема:Если пространственная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой точки равен геометрической сумме моментов всех сил этой системы относительно той же точки:

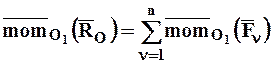. (4.29)

Доказательство: Пусть система сил 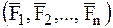приводится к равнодействующей, которая приложена в точке О, тогда, используя основную теорему статики, получим:

' ,

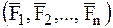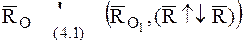где на основании (4.2) .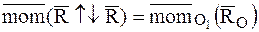

С другой стороны, приведя пространственную систему сил к центру О₁ на основании соотношения (4.6) получим:

.

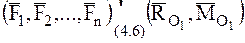Сравнивая оба выражения, можно записать, с учетом соотношения (4.4):

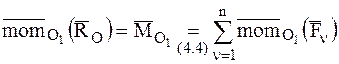, что и требовалось доказать.