Зависимость (5.3) выражает закон вязкого трения Ньютона и справедлива при слоистом (ламинарном) течении жидкости.

В практических расчетах часто используют кинематический коэффициент вязкости

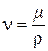. (5.5)

Ниже приводятся значения 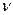для некоторых жидкостей и газов. Для воды, керосина и глицерина соответственно (при 18ºС) 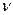= 0,0106 см²/с; 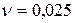см²/с; 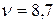см²/с. Для воздуха и для метана соответственно 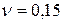см²/с, 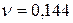см²/с.

Поверхностное натяжение проявляется в поверхностном слое жидкости и обусловлено особенностями взаимодействия молекул, образующих этот слой; это свойство жидкости характеризуется коэффициентом поверхностного натяжения. Влияние поверхностного натяжения обычно не учитывают, однако в трубах малого диаметра не считаться с ним нельзя. В узких трубках жидкость поднимается на высоту

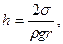
где σ – коэффициент поверхностного натяжения (для воды 0,0726 Н/м при 20 ºС); r – радиус трубки; g – ускорение свободного падения; 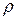– плотность жидкости.

Идеальная жидкость. В гидравлике используют различные упрощенные модели среды; одной из таких моделей является идеальная жидкость. Под идеальной жидкостью понимают воображаемую жидкость, обладающую абсолютной подвижностью (т.е. лишенной вязкости), абсолютно несжимаемую. Для идеальной жидкости 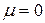и и 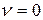при движении ее трение отсутствует.

Задача 5.1.В технике давление часто измеряется в атмосферах; перевести 1 ат в Паскали (Па).

Решение. Сила 1 кГ эквивалентна 9,8 Н, поэтому последовательно можно записать
1 ат = 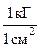= = 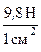= = 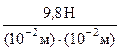= = 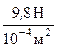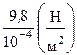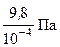9,8·10⁴ Па.

Задача 5.2.Давление в баллоне с ацетиленом для газовой сварки при хранении его вне помещения при температуре 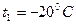равно 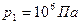.Каково будет давление в баллоне при внесении в его помещение, где температура равна ?

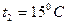Решение. Так как объём баллона и масса газа в нём при внесении его в помещение не изменились, то и плотность газа в соответствии с (5.1) осталась неизменной, т.е. 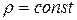.Тогда из уравнения (5.5) следует: 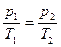и после подстановки числовых значений: 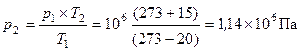. Как следует из решения, от рода газа результат не зависит.

Уравнение состояния. Давление жидкости (или газа) р меняется с изменением ее плотности 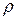и температуры Т. Соотношение 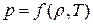называется уравнением состояния. Для капельных жидкостей в гидравлических расчетах уравнение состояния принимают в предельно простой форме: 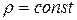(т.е. плотность капельных жидкостей неизменна).

Для газов уравнение состояния имеет вид:

,

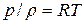где р – абсолютное давление; Т – термодинамическая температура, для воздуха R=287 Дж/(кг·К).