Основное уравнение молекулярно-кинетической теории идеальных газов
Рассмотрим одноатомный идеальный газ, занимающий некоторый объем. Выделим на стенке сосуда некоторую элементарную площадку ∆S и вычислим давление, оказываемое молекулами газа на эту площадку. Каждая молекула при соударении передает площадке  импульс, равный изменению импульса молекулы
импульс, равный изменению импульса молекулы 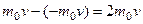 . За время
. За время 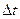 площадки
площадки  могут достигнуть только те молекулы, которые заключены в объеме цилиндра с основанием
могут достигнуть только те молекулы, которые заключены в объеме цилиндра с основанием  и высотой
и высотой 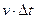 . Это число молекул равно
. Это число молекул равно 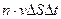 .Столкновениями молекул между собой пренебрегаем. Хаотическое движение молекул заменяют движением в трех взаимно перпендикулярных направлениях вдоль осей x, y,z.
.Столкновениями молекул между собой пренебрегаем. Хаотическое движение молекул заменяют движением в трех взаимно перпендикулярных направлениях вдоль осей x, y,z.
Вдоль каждого из них движется 1/3 молекул, 1/6 часть в одном направлении и 1/6 в противоположном. При столкновении с площадкой они передадут ей импульс:
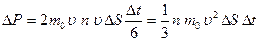
где 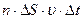 - число молекул в объеме цилиндра, с основанием ∆S;
- число молекул в объеме цилиндра, с основанием ∆S; 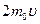 - изменение импульса одной молекулы
- изменение импульса одной молекулы
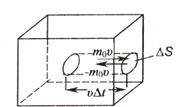
при соударении со стенкой (рис.18).
 По второму закону Ньютона
По второму закону Ньютона 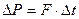 ,
,
где F – сила, действующая на стенку площадью ∆S.
Давление газа на стенку 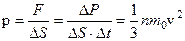 .
.
рис.18
Молекулы газа движутся с различными скоростями v1, v2….vn , поэтому на основании статистического метода необходимо рассматривать среднюю квадратичную скорость движения молекул.
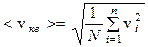
Если  , где N – общее число молекул, V – объем,
, где N – общее число молекул, V – объем,
то 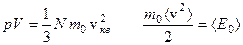 – кинетическая энергия одной молекулы, m0 – масса молекулы.
– кинетическая энергия одной молекулы, m0 – масса молекулы.
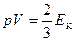 ,
,
где ЕК – кинетическая энергия всех молекул.
Это основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса). Используя уравнение Клапейрона – Менделеева можно получить выражение для Е0:
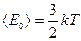
Дата добавления: 2015-08-01; просмотров: 655;
