Дифракция от прямоугольной щели

Различают два вида дифракции: дифракцию в параллельных лучах (дифракция Фраунгофера) и сходящихся лучах (дифракция Френеля).

Рассмотрим дифракцию Фраунгофера на узкой прямоугольной щели. Пусть пучок параллельных лучей монохроматического света падает перпендикулярно на узкую прямоугольную щель шириной 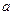в непрозрачном экране Э₁ (рис.6). За щелью расположена линза 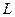, которая собирает лучи на экране Э₂, помещенном в ее фокальной плоскости (рис.7). Если бы при прохождении света через щель соблюдался закон прямолинейного распространения света, то на экране Э₂ получилось бы изображение прямоугольной щели.

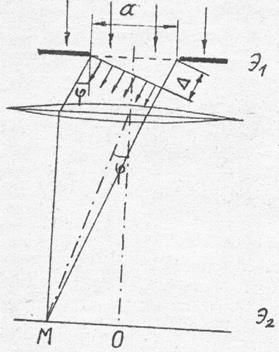
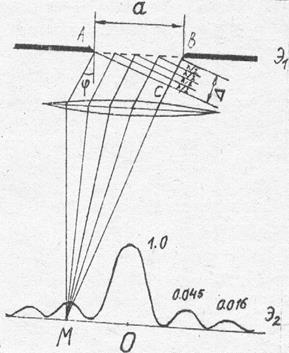
Рис.6 Рис.7

Вследствие дифракции картина коренным образом изменяется: на экране наблюдается система интерференционных максимумов – размытых изображений щели, разделенных темными промежутками интерференционных минимумов.

Согласно принципу Гюйгенса, каждый элемент поверхности световой волны АВ является источником когерентных волн, распространяющихся в различных направлениях. Из всех возможных направлений выберем одно – под углом 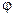относительно нормали к плоскости щели. Лучи, идущие из разных участков щели АВ под углом 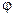по отношению к их первоначальному направлению, соберутся линзой в точке М. Они пройдут разные пути и будут сдвинуты по фазе. Результат их интерференции в точке М зависит от угла 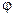и ширины щели.

Для объяснения полученной картины воспользуемся методом зон Френеля и выполним следующее построение. Через крайнюю точку А щели (см. рис.7) проведем плоскость АС, перпендикулярную направлению дифрагированных лучей. Тогда отрезок ВС будет представлять собой раз-ность хода крайних-лучей. Разделим его на ряд отрезков длиной 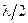. Число таких отрезков 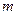будет равно

(4)

Через концы этих отрезков проведем плоскости, параллельные плоскости АС, до пересечения с открытой частью волновой поверхности АВ. Фронт волны АВ разобьется на 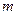полосок одинаковой ширины, являющихся зонами Френеля. Колебания, приходящие в точку М от любой пары соседних зон, имеют разность хода 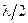и, находясь в противоположных фазах, ослабляют друг друга. Следовательно, ослабление света (дифракционный минимум) в точке М наблюдается при четном числе 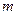( 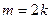), а усиление (дифракционный максимум) – при нечетном числе 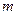( 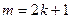). Таким образом, из формулы (4) получим условия минимумов и максимумов освещенности:

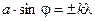(5)

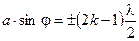(6)

где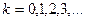

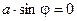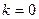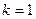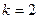Дифракционная картина от одной щели представляет собой чередование светлых и темных полос около нейтрального максимума, которому соответствует условие . Число и называется порядком, дифракционного максимума: числу соответствует максимум нулевого порядка, числам и – максимумы первого и второго порядков соответственно. На рис.7 указаны положение и интенсивности дифракционных максимумов. Область, лежащую между 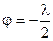и 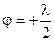, занимает центральная светлая полоса. Чем меньше длина волны и больше ширина щели, тем уже эта полоса. Положение максимумов и минимумов на экране Э₂ зависят от длины падающей световой волны, Если падающий свет сложный, например, состоит из двух монохроматических излучений с длинами волн 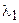и 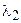, то на экране максимумы и минимумы этих волн располагаются а разных местах. Большим 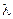соответствуют большие углы отклонения.