Усеченное нормальное распределение

Известно, что корректность использования классического нормального распределения наработки, достигается при Т₀ 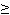3S.

При малых значениях Т₀ и большом S, может возникать ситуация, когда ПРО f(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4).

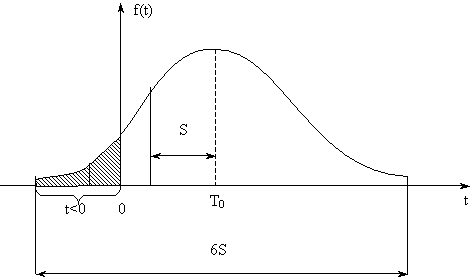
Рис.6.4

Таким образом, нормальное распределение являясь общим случаем распределения случайной величины в диапазоне (- 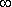; 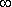), лишь в частности (при определенных условиях) может быть использовано для моделей надежности.

Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений наработки до отказа.

В общем случае усечение может быть:

· левым – (0; );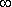

· двусторонним – (t₁ , t₂).

Смысл усеченного нормального распределения (УНР) рассмотрен для случая ограничения случайной величины наработки интервалом (t₁ , t₂).

Плотность УНР 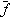(t) = c f(t) ,

где

c – нормирующий множитель, определяемый из условия, что площадь под кривой 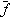(t) равна 1, т. е.

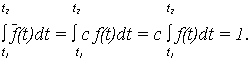
Откуда

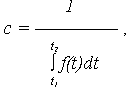
где

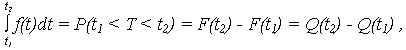
Применяя переход от случайной величины Т = {t} к величине X = {x}:

x₂ = (t₂ – Т₀)/S ; x₁ = (t₁ – Т₀)/S ,

получается

поэтому нормирующий множитель c равен:

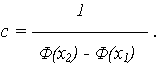
Поскольку [ 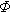(x)(x₂) - 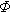(x)(x₁)] < 1, то c > 1, поэтому 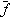(t)> f(t). Кривая 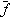(t) выше, чем f(t), т. к. площади под кривыми 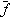(t) и f(t) одинаковы и равны 1 (рис. 5).

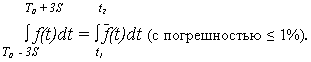
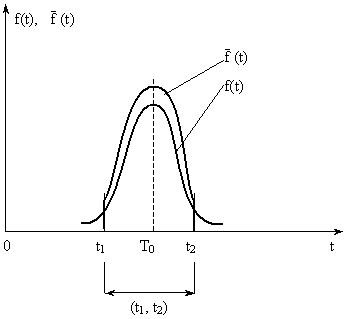
Рис. 6.5

Показатели безотказности для УНР в диапазоне (t₁ , t₂):

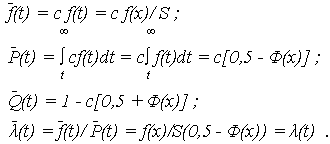
УНР для положительной наработки до отказа – диапазон (0; 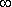) имеет ПРО

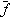(t) = c₀ f(t) ,

где c₀ – нормирующий множитель определяется из условия:

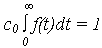
и равен (аналогично предыдущему):

Показатели безотказности УНР (0; )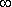

Изменение нормирующего множителя c₀ в зависимости от отношения Т₀ /S приведено на рис. 6.

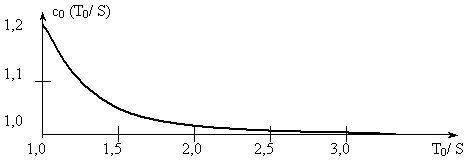Рис. 6.6.

При Т₀ = S, Т₀ / S = 1 c₀ = max ( 1,2) .

При Т₀ / S 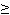2,5 c₀ = 1,0, т.е. 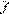(t)(t) = f(t) .

Контрольные вопросы и задачи:

1. Объясните почему распределение Гаусса называется нормальным?

2. Поясните на изменении кривой плотности распределения отказов влияние параметров распределения: матожидания и дисперсии?

3. Приведите расчетные выражения для показателей безотказности, определенные через табличные функции: f(x), F(x) и 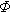(x)?

4. При каких условиях корректно использовать классическое нормальное распределение, и в каких случаях целесообразно применять усеченные нормальные распределения?

5. Приведите расчетные выражения показателей безотказности для усеченного «слева» нормального распределения?

6. Наработка до отказа серийно выпускаемой детали распределена нормально с параметрами: Т₀ = M(T) = 104 час, S = S (T) = 250 час. Определить:

1) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [5000, 9000 час];

2) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [Т₀ - 3S, Т₀ + 3S];

3) вероятность того, что безотказно проработав до момента времени 5000 час, деталь безотказно проработает и до 9000 час?

Ответы: 1) 0.00003, 2) 0.9974, 3) 0.99997.

7. Комплектующая деталь, используемая при изготовлении устройства, по данным поставщика этой детали имеет нормальное распределение наработки с параметрами:

Т₀ = 4 · 103 час, S = 800 час. Определить интересующую конструктора прибора:

1) наработку до отказа, соответствующую 90% надежности детали;

2) вероятность того, что при монтаже деталь имеет наработку, лежащую в интервале [2.5 · 103, 3 · 103];

3) вероятность того, что при монтаже деталь имеет наработку, большую, чем 2.5 103 час?

Ответы: 1) 2974.4, 2) 0.0755, 3) 0.9699.

Глава 7.ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НАРАБОТКИ ДО ОТКАЗА: ЭКСПОНЕНЦИАЛЬНЫЙ, ЛОГНОРМАЛЬНЫЙ И ГАММА-РАСПРЕДЕЛЕНИЕ