Следствия основных теорем

Следствия основных теорем - формула полной вероятности (ФПВ) и формула Байеса находят широкое применение при решении большого числа задач.

Формула полной вероятности.

Если по результатам опыта можно сделать n исключающих друг друга предположений (гипотез) H₁, H₂, … H_n, представляющих полную группу несовместных событий (для которой P(i)=1), то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:

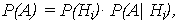
(13)

где P(Hi) – вероятность гипотезы Hi;

P(А| Hi) – условная вероятность события А при гипотезе Hi.

Поскольку событие А может появиться с одной из гипотез H₁, H₂, … H_n, то А= АH₁ 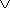АH₂ 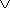… 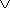АH_n , но H₁, H₂, … H_n несовместны, поэтому

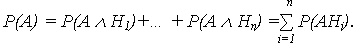
При зависимости события А от появления гипотезы Hi P(AHi) = P(Hi)· P(А| Hi), откуда и следует выражение (13).

Формула Байеса (формула вероятностей гипотез).

Если до опыта вероятности гипотез H₁, H₂, … H_n были равны P(H₁), P(H₂), …, P(H_n), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:

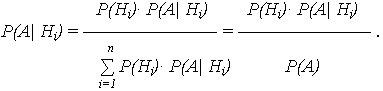
(14)

Доопытные (первоначальные) вероятности гипотез P(H₁), P(H₂), …, P(H_n) называются априорными, а послеопытные - P(H₁| А), … P(H_n| А) – апостериорными.

Формула Байеса позволяет «пересмотреть» возможности гипотез с учетом полученного результата опыта.

Доказательство формулы Байеса следует из предшествующего материала. Поскольку P(Hi 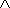А) = P(Hi)· P(А| Hi) = P(Hi)· P(Hi| А):

(15)

откуда, с учетом (13), получается выражение (15).

Если после опыта, давшего событие А, проводится еще один опыт, в результате которого может произойти или нет событие А₁, то условная вероятность этого последнего события вычисляется по (13), в которую входят не прежние вероятности гипотез P(Hi), а новые - P(Hi| А):

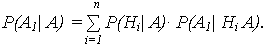
(16)

Выражение (16) называют формулой для вероятностей будущих событий.

Контрольные вопросы и задачи:

1. Перечислите показатели безотказности объекта и поясните, чем отличаются статистическая (выборочные оценки) и вероятностная форма (определения)?

2. Поясните «схему испытаний» объекта при определении выборочных оценок показателей безотказности?

3. Дайте определение «оценки» вероятности события и объясните условие сходимости оценки и вероятности события?

4. Перечислите и поясните основные аксиомы вероятности?

5. Перечислите и поясните смысл основных правил (теорем) теории вероятностей?

6. Назовите следствия основных теорем теории вероятностей?

7. Прибор может работать в двух режимах: «1» и «2». Режим «1» наблюдается в 80% случаев, режим «2» - в 20% случаев за время работы T. Вероятность того, что прибор откажет при работе в режиме «1» равна 0.1, а вероятность отказа прибора в режиме «2» - 0.7. Найти вероятность отказа прибора за время T? Ответ: 0.22

8. Прибор состоит из 3-х блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0.2, второй – 0.1, третий – 0.3. Найти вероятность того, что за время T прибор проработает безотказно?

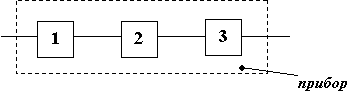
Ответ: 0.504

9. Прибор состоит из 2-х блоков, дублирующих друг друга. Вероятность того, что за время T каждый из блоков проработает безотказно, равна 0.9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что за время T прибор проработает безотказно?

Ответ: 0.99