Синтез абстрактных автоматов

Любой абстрактный автомат можно представить в виде дискретного устройства, которое имеет N входов и K выходов, кроме того, такое дискретное устройство может иметь S обратных связей, проходящих через устройства задержки (см. рис.3).

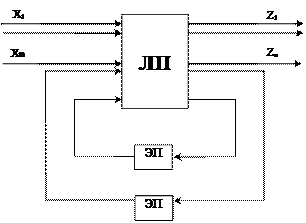
Часть устройства, в котором сосредоточены логические элементы (элементы без памяти), называют логическим преобразователем (ЛП). На входы элементов памяти, выступающих в роли элементов задержки, воздействуют сигналы, снимаемые с дополнительных (внутренних) выходов ЛП. Будем предполагать, что каждый элемент памяти будет находиться в двух состояниях: 0 и 1. Каждый элемент памяти может сохранить 2^s состояний.

При двузначных значениях входных сигналов (0, 1) число различных входных состояний будет равно 2^N. Говорят, что i-ый набор (i 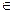[1,n]) значений входных аргументов, воздействуют на различные входы ЛП и образует состояние входа .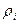

Аналогично число состояний выходов определяется значениями выходных аргументов 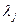, где j 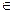[1,к].

Состояния всех элементов памяти определяет состояние автомата. S_M – число возможных внутренних состояний автомата.

Конечным автоматом называется устройство, определенное конечным множеством состояний входов – 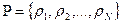, конечным множеством состояний выходов - 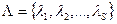, конечным множеством внутренних состояний 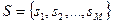, а также функцией переходов. определяющей порядок смен внутренних состояний ( 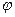) и функцией выходов, задающих выходные состояния в зависимости от 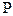и ( ).

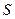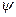S =

Из множества внутренних состояний выделяется некоторое начальное состояние, называемое начальным внутренним состоянием автомата.

Будем предполагать, что автомат функционирует в некоторые дискретные моменты времени (такт). Время, в течение которого не происходит изменение входного сигнала 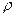, обозначается через T и в зависимости от того, чем определяется длительность этого интервала, будем различать два класса автоматов: синхронные и асинхронные.