Формула (3) называется координатным выражением векторного произведения .
Замечание. Если требуется найти векторное произведение 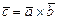 векторов
векторов 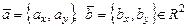 , то сначала векторы
, то сначала векторы 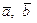 переносят в пространство
переносят в пространство 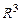 :
:
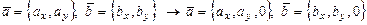 , а затем используют формулу (3), которая в данном случае дает:
, а затем используют формулу (3), которая в данном случае дает:
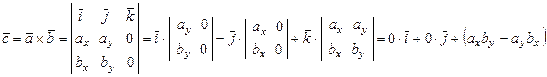 ,
,
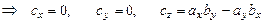 .
.
Пример 5. Найти 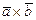 , если
, если 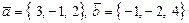 .
.
Решение. 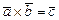 . Координаты вектора
. Координаты вектора 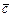 найдем с помощью формулы (3).
найдем с помощью формулы (3).
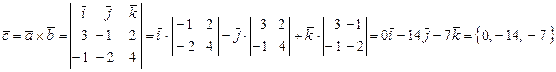 .
.
Пример 6. Найти площадь параллелограмма, построенного на векторах 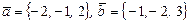 .
.
Решение. Сначала найдем векторное произведение 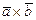 .
.
 . Ош!
. Ош!
Теперь воспользуемся геометрическим смыслом векторного произведения, по которому длина вектора 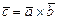 равна искомой площади
равна искомой площади 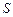 параллелограмма на векторах
параллелограмма на векторах 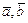 , т.е.
, т.е.
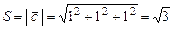 .
.
Пример 7. Найти площадь треугольника 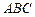 на плоскости
на плоскости 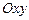 с вершинами в точках
с вершинами в точках 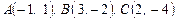 .
.
Решение. Рассмотрим векторы 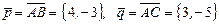 . Найдем их векторное произведение
. Найдем их векторное произведение 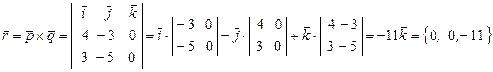 .
.
Площадь 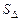 треугольника
треугольника 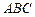 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 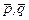 . Следовательно,
. Следовательно, 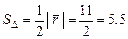 .
.
Пример 8. Найти координаты орта 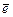 , перпендикулярного одновременно векторам
, перпендикулярного одновременно векторам 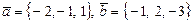 и такого, чтобы тройка
и такого, чтобы тройка 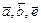 была правой.
была правой.
Решение. Сначала с помощью формулы (3) найдем вектор 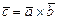 .
.
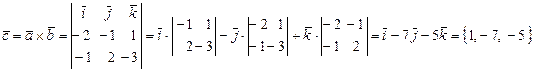 .
.
Согласно определению вектор 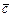 перпендикулярен одновременно векторам
перпендикулярен одновременно векторам 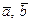 и тройка
и тройка
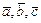 - правая. Проверим перпендикулярность пар векторов:
- правая. Проверим перпендикулярность пар векторов: 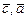 и
и 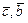 , используя условие ортогональности векторов (см. Занятие 6.)
, используя условие ортогональности векторов (см. Занятие 6.)
1) 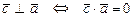 .
. 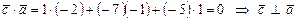 .
.
2) 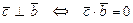 .
. 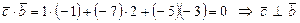 .
.
Искомый орт 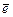 получается нормировкой вектора
получается нормировкой вектора 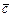 .
. 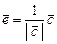 .
. 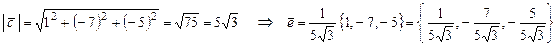 .
.
Пример 9. Сформулировать условие коллинеарности векторов с помощью векторного произведения.
Решение.
1). Если 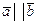 , то угол
, то угол 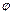 между
между 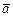 и
и 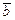 равен 0 или
равен 0 или 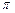 . Рассмотрим
. Рассмотрим 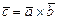 .
.
Согласно требованию 3 и указанным значениям угла 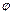 из определения векторного произведения выводим:
из определения векторного произведения выводим: 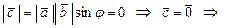
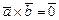 .
.
2). Рассмотрим теперь векторное равенство 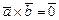 . В силу определения векторного произведения (достаточно использовать требование 3) из этого векторного равенства получаем следующие три возможности: а)
. В силу определения векторного произведения (достаточно использовать требование 3) из этого векторного равенства получаем следующие три возможности: а) 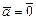 ; б)
; б) 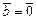 ; в)
; в) 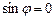 , т.е.
, т.е. 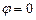 или
или 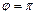 . Т.к. нулевой вектор параллелен любому вектору, то все три случая а), б), в) приводят к выводу:
. Т.к. нулевой вектор параллелен любому вектору, то все три случая а), б), в) приводят к выводу: 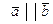 .
.
Таким образом, условие коллинеарности можно записать в виде: 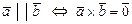 .
.
Отсюда, как следствие получаем: 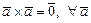 .
.
7.4. Смешанное произведение: определение; свойства; координатное выражение. Условие компланарности тройки векторов.
Смешанное произведение определено на трех векторах 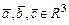 . Обозначим его
. Обозначим его 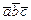 .
.
Определение.  . Таким образом, смешанное произведение векторов
. Таким образом, смешанное произведение векторов 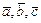 представляет векторное произведение векторов
представляет векторное произведение векторов 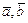 , умноженное затем скалярно на вектор
, умноженное затем скалярно на вектор 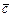 . Результатом смешанного произведения векторов будет число.
. Результатом смешанного произведения векторов будет число.
Свойства смешанного произведения.
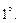
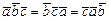 .
.
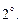
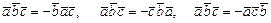 .
.
Перестановки векторов: 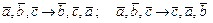 называются циклическими.
называются циклическими.
Свойства 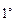 ,
, 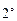 означают, что смешанное произведение векторов не меняется после циклической перестановки векторов и изменяет свое значение на противоположное при нециклических перестановках векторов.
означают, что смешанное произведение векторов не меняется после циклической перестановки векторов и изменяет свое значение на противоположное при нециклических перестановках векторов.
Если векторы заданы координатами 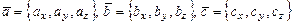 , то смешанное произведение
, то смешанное произведение 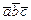 находится по формуле
находится по формуле
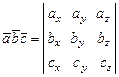 . (4)
. (4)
Эта формула дает координатное выражение смешанного произведения 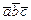 .
.
Смешанное произведение 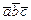 имеет следующий геометрический смысл:
имеет следующий геометрический смысл:
1. Если тройка векторов 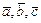 -правая, то смешанное произведение
-правая, то смешанное произведение 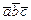 равно объему
равно объему 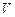 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах 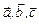 ;
;
2. Если же тройка 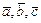 - левая, то
- левая, то 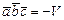 , где
, где 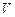 - объем параллелепипеда на векторах
- объем параллелепипеда на векторах 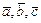 .
.
Указанный геометрический смысл смешанного произведения векторов приводит к следующей формулировке условия компланарности системы из трех векторов 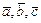 :
:
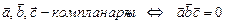 . (5)
. (5)
Пример 10. Вычислить 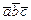 , если
, если 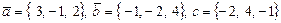 .
.
Решение. Согласно координатному выражению (4) находим
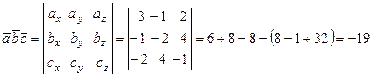 .
.
Заметим, что полученный результат позволяет также сказать, что
1) тройка 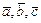 - левая (т.к.
- левая (т.к. 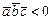 ) и
) и
2) объем параллелепипеда на векторах 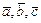 равен 19.
равен 19.
Пример 11. Найти объем пирамиды 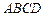 с вершинами
с вершинами 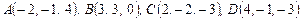 .
.
Решение. Рассмотрим векторы  .ош!
.ош!
Найдем их смешанное произведение.
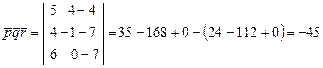 .
.
Следовательно, объем 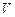 параллелепипеда на векторах
параллелепипеда на векторах 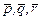 равен 45. Объем
равен 45. Объем 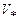 пирамиды
пирамиды 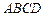 составляет одну шестую объема
составляет одну шестую объема 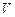 . Таким образом,
. Таким образом, 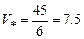 .
.
Пример 12. Выяснить, лежат ли точки 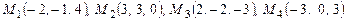
на одной плоскости.
Решение. Четыре произвольно выбранные точки в общем случае не лежат одной плоскости. Для того, чтобы заданные четыре точки оказались на одной плоскости нужно, чтобы тройка векторов 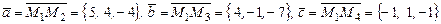 была компланарной. Условие компланарности :
была компланарной. Условие компланарности : 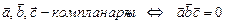 .
.
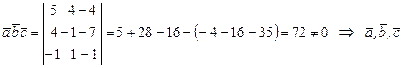 - не компланарны
- не компланарны 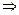
заданные точки 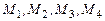 не лежат на одной плоскости.
не лежат на одной плоскости.
____________________________________________________________________________
Домашнее задание.
1. Найти координаты вектора 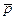 , удовлетворяющего следующим условиям:
, удовлетворяющего следующим условиям:
а) 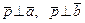 ; б)
; б) 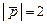 ; в)
; в) 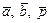 - левая тройка, если
- левая тройка, если 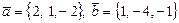 .
.
2. Вычислить площадь треугольника 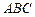 с вершинами
с вершинами 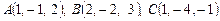 .
.
3. Найти объем пирамиды 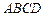 с вершинами
с вершинами 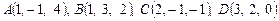 .
.
4. При каком значении параметра 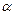 точки
точки 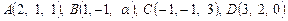 лежат в одной плоскости?
лежат в одной плоскости?
| <== предыдущая лекция | | | следующая лекция ==> |
| Если в ходе проведения метода Гаусса появляются невыполнимые равенства типа и т.д., то исследуемая линейная система несовместна. | | | НАЗНАЧЕНИЕ ПРИПУСКОВ НА МЕХАНИЧЕСКУЮ ОБРАБОТКУ. |
Дата добавления: 2015-07-30; просмотров: 808;
